Работа с признаками как часть машинного обучения
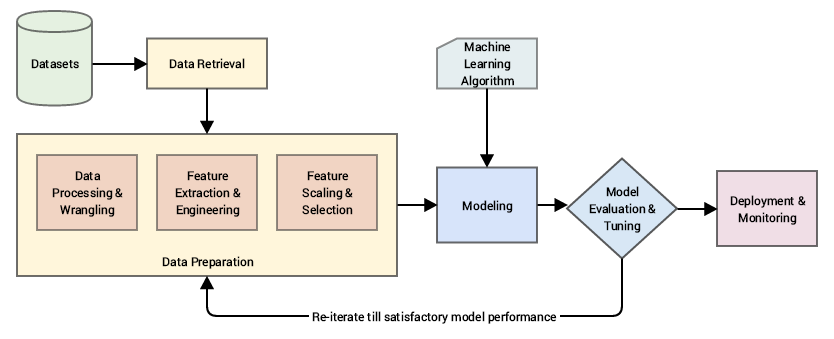
Selecting variables for modeling is "one of the most creative parts of the data mining process
Data Mining Techniques, Gordon Linoff and Michael Berry
Определение
Признак (фича, feature) - это индивидуальное измеримое свойство или характеристика наблюдаемого явления (Bishop, 2006). Примеры признаков — пол, цвет, цена и т.д.
Конструирование признаков — это процесс трансформации существующих признаков или создания на их основе новых с целью улучшения работы алгоритмов машинного обучения.
Coming up with features is difficult, time-consuming, requires expert knowledge. "Applied machine learning" is basically feature engineering.
Andrew Ng, Machine Learning and AI via Brain simulations
Обучение признакам или обучение представлениям — это набор техник, которые позволяют системе автоматически обнаружить представления, необходимые для выявления признаков или классификации исходных (сырых) данных. Это заменяет ручное конструирование признаков и позволяет машине как изучать признаки, так и использовать их для решения специфичных задач.
- Representation Learning: A Review and New Perspectives
- An overview on data representation learning: From traditional feature learning to recent deep learning
Выделение признаков — это разновидность абстрагирования, процесс снижения размерности, в котором исходный набор исходных переменных сокращается до более управляемых групп (признаков) для дальнейшей обработки, оставаясь при этом достаточным набором для точного и полного описания исходного набора данных. Примеры алгоритмов выделения признаков:
- Independent component analysis
- PCA
- Latent semantic analysis
- Principal component analysis
- Autoencoder
Типы данных
Шклассификация шкал:
- Простая номинальная шкала
- Частично упорядоченная шкала
- Порядковая (ранги, бальных оценок)
- Метрические равных интервалов
- Пропорциональных оценок.
Другие типы
- ID
- Счётные данные
- Даты
- Текст
- Координаты
Практика
- Feature Engineering for Machine Learning Principles and Techniques for Data Scientists
- Understanding Feature Engineering (Part 1) — Continuous Numeric Data
- Пример Feature Engineering в машинном обучении
- Открытый курс машинного обучения. Тема 6. Построение и отбор признаков, en.
- SciKit-Learn preprocessing data
- About Feature Scaling and Normalization – and the effect of standardization for machine learning algorithms
- Discover Feature Engineering, How to Engineer Features and How to Get Good at It
- Методы отбора фич
- Методические заметки об отборе информативных признаков (feature selection)
- Как попасть в топ 2% соревнования Kaggle
Работа с метрическими признаками
Монотонное преобразование признаков критично для одних алгоритмов и не оказывает влияния на другие. Кстати, это одна из причин популярности деревьев решений и всех производных алгоритмов (случайный лес, градиентный бустинг) – не все умеют/хотят возиться с преобразованиями, а эти алгоритмы устойчивы к необычным распределениям.
Бывают и сугубо инженерные причины: логарифмирование как способ борьбы со слишком большими числами, не помещающимися в память. Но это скорее исключение, чем правило; чаще все-таки вызвано желанием адаптировать датасет под требования алгоритма. Параметрические методы обычно требуют как минимум симметричного и унимодального распределения данных, что не всегда обеспечивается реальным миром. Могут быть и более строгие требования (уместно вспомнить урок про линейные модели).
Впрочем, требования к данным предъявляют не только параметрические методы: тот же метод ближайших соседей предскажет полную чушь, если признаки ненормированы: одно распределение расположено в районе нуля и не выходит за пределы (-1, 1), а другой признак – это сотни и тысячи.
Квантование
В обработке сигналов — разбиение диапазона отсчётных значений сигнала на конечное число уровней и округление этих значений до одного из двух ближайших к ним уровней.
Бинаризация
Всё просто — выбираем порог, значениям ниже которого присваивается одно значение, а выше — другое.
Биннинг, он же бакетинг
Это техника обработки данных, при которой исходный набор данных делится на некоторое количество интервалов, общее значение которых (обычно среднее) затем представляет все значения интвервала, что позволяет уменьшить влияние отдельных наблюдений. Иными словами мы переводим непрерывную величину в дискретную. Техника бининга используется для простоения гистограмм.
Ключевым вопросом в бининге является решение относительно длины интервалов. Интервалы могут быть фиксированной или адаптивной длины.
Приведите пример фиксированного биннига? В каких случаях его лучше использовать?
from scipy import stats import pandas as pd import numpy as np import json import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline small_counts = np.random.randint(0, 100, 20) small_counts
62, 82, 54])
Равнораспределённый бининг 0-9.
np.floor_divide(small_counts, 10)
Данные могут быть распределены очень неравномерно
large_counts = [296, 8286, 64011, 80, 3, 725, 867, 2215, 7689, 11495, 91897, 44, 28, 7971, 926, 122, 22222]
sns.barplot(y=large_counts, x=list(range(len(large_counts))))
Тогда имеет смысл делать логарифмированный фиксированный бининг:
log_bining = np.floor(np.log10(large_counts)) log_bining
sns.barplot(y=log_bining, x=list(range(len(log_bining))))
В общем-то, это обычное логарифмирование
Квантилизация
Квантилизация — это адаптивный бининг, основанный на распределении данных. Если в обычном биннинге могут быть пустые интервалы, то здесь — нет.
pd.qcut(large_counts, 4, labels=False)
biz_f = open('data/yelp_academic_dataset_business.json') biz_df = pd.DataFrame([json.loads(x) for x in biz_f.readlines()]) biz_f.close()
biz_df.head()
| business_id | categories | city | full_address | latitude | longitude | name | neighborhoods | open | review_count | stars | state | type | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | rncjoVoEFUJGCUoC1JgnUA | [Accountants, Professional Services, Tax Servi... | Peoria | 8466 W Peoria Ave\nSte 6\nPeoria, AZ 85345 | 33.581867 | -112.241596 | Peoria Income Tax Service | [] | True | 3 | 5.0 | AZ | business |
| 1 | 0FNFSzCFP_rGUoJx8W7tJg | [Sporting Goods, Bikes, Shopping] | Phoenix | 2149 W Wood Dr\nPhoenix, AZ 85029 | 33.604054 | -112.105933 | Bike Doctor | [] | True | 5 | 5.0 | AZ | business |
| 2 | 3f_lyB6vFK48ukH6ScvLHg | [] | Phoenix | 1134 N Central Ave\nPhoenix, AZ 85004 | 33.460526 | -112.073933 | Valley Permaculture Alliance | [] | True | 4 | 5.0 | AZ | business |
| 3 | usAsSV36QmUej8--yvN-dg | [Food, Grocery] | Phoenix | 845 W Southern Ave\nPhoenix, AZ 85041 | 33.392210 | -112.085377 | Food City | [] | True | 5 | 3.5 | AZ | business |
| 4 | PzOqRohWw7F7YEPBz6AubA | [Food, Bagels, Delis, Restaurants] | Glendale Az | 6520 W Happy Valley Rd\nSte 101\nGlendale Az, ... | 33.712797 | -112.200264 | Hot Bagels & Deli | [] | True | 14 | 3.5 | AZ | business |
sns.set_style('whitegrid') fig, ax = plt.subplots() biz_df['review_count'].hist(ax=ax, bins=100) ax.set_yscale('log') ax.tick_params(labelsize=14) ax.set_xlabel('Review Count', fontsize=14) ax.set_ylabel('Occurrence', fontsize=14)
deciles = biz_df['review_count'].quantile([.1, .2, .3, .4, .5, .6, .7, .8, .9]) deciles
0.2 3.0
0.3 4.0
0.4 5.0
0.5 6.0
0.6 8.0
0.7 12.0
0.8 23.0
0.9 50.0
Name: review_count, dtype: float64
sns.set_style('whitegrid') fig, ax = plt.subplots() biz_df['review_count'].hist(ax=ax, bins=100) for pos in deciles: handle = plt.axvline(pos, color='r') ax.legend([handle], ['deciles'], fontsize=14) ax.set_yscale('log') ax.set_xscale('log') ax.tick_params(labelsize=14) ax.set_xlabel('Review Count', fontsize=14) ax.set_ylabel('Occurrence', fontsize=14)
Рангова трансформация
biz_df['review_count'].rank().head()
1 4756.5
2 3386.0
3 4756.5
4 8344.0
Name: review_count, dtype: float64
То же в scipy
from scipy.stats import rankdata rankdata(biz_df['review_count'].values)
Преобразования, стабилизирующие дисперсию
Многие типы статистических данных обнаруживают связь «дисперсии и среднего», что означает — изменчивость различна для значений данных с различными математическими ожиданиями. В качестве примера, при сравнении различных популяций в мире увеличение дисперсии доходов приводит к увеличению математического ожидания доходов. Если мы рассматриваем число маленьких единиц площади (например, административные округа в Соединённых Штатах Америки) и получим среднее и дисперсию доходов для каждого округа, обычно получим, что округа с большим средним доходом имеют большую дисперсию.
Преобразование, стабилизирующее дисперсию нацелено на удаление связи дисперсии и математического ожидания, так что дисперсия становится постоянной относительно среднего.
Степенные преобразования
Степенные преобразования нацелены на стабилизацию дисперсии случайной величины.
p = np.random.poisson(size=10000) ax = sns.distplot(p, kde=False) ax.set(xlabel='Poisson', ylabel='Frequency');
Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
Логарифмирование
Логарифмирование — частный случай степенных преобразований.
biz_df["log_review_count"] = np.log10(biz_df['review_count'] + 1)
plt.figure() ax = plt.subplot(2,1,1) biz_df['review_count'].hist(ax=ax, bins=100) ax.tick_params(labelsize=14) ax.set_xlabel('review_count', fontsize=14) ax.set_ylabel('Occurrence', fontsize=14) ax = plt.subplot(2,1,2) biz_df["log_review_count"].hist(ax=ax, bins=100) ax.tick_params(labelsize=14) ax.set_xlabel('log10(review_count))', fontsize=14) ax.set_ylabel('Occurrence', fontsize=14)
from sklearn import linear_model from sklearn import cross_validation
biz_train, biz_validate = cross_validation.train_test_split(biz_df, test_size=0.2)
m1 = linear_model.LinearRegression() m1.fit(biz_train[['log_review_count']], biz_train['stars']) m2 = linear_model.LinearRegression() m2.fit(biz_train[['review_count']], biz_train['stars'])
print("Residual sum of squares: {:.3f}".format( np.mean((m1.predict(biz_validate[['log_review_count']]) - biz_validate['stars']) ** 2)))
print("Residual sum of squares: {:.3f}".format( np.mean((m2.predict(biz_validate[['review_count']]) - biz_validate['stars']) ** 2)))
Трансформация Бокса-Кокса
Для исходной последовательности y = { y_1, \ldots, y_n }, \quad y_i > 0, \quad i = 1,\ldots,n однопараметрическое преобразование Бокса-Кокса с параметром определяется следующим образом:
Параметр можно выбирать, максимизируя логарифм правдоподобия. Еще один способ поиска оптимального значения параметра основан на поиске максимальной величины коэффициента корреляции между квантилями функции нормального распределения и отсортированной преобразованной последовательностью.
rc_log = stats.boxcox(biz_df['review_count'], lmbda=0) # from sklearn.preprocessing import power_transform # By default, the scipy implementation of Box-Cox transform finds the lmbda parameter # that will make the output the closest to a normal distribution rc_bc, bc_params = stats.boxcox(biz_df['review_count']) bc_params
biz_df['rc_bc'] = rc_bc biz_df['rc_log'] = rc_log
fig, (ax1, ax2, ax3) = plt.subplots(3,1) fig.set_size_inches(18.5, 10.5) # original review count histogram biz_df['review_count'].hist(ax=ax1, bins=100) ax1.set_yscale('log') ax1.tick_params(labelsize=14) ax1.set_title('Review Counts Histogram', fontsize=14) ax1.set_xlabel('') ax1.set_ylabel('Occurrence', fontsize=14) # review count after log transform biz_df['rc_log'].hist(ax=ax2, bins=100) ax2.set_yscale('log') ax2.tick_params(labelsize=14) ax2.set_title('Log Transformed Counts Histogram', fontsize=14) ax2.set_xlabel('') ax2.set_ylabel('Occurrence', fontsize=14)# review count after optimal Box-Cox transform biz_df['rc_bc'].hist(ax=ax3, bins=100) ax3.set_yscale('log') ax3.tick_params(labelsize=14) ax3.set_title('Box-Cox Transformed Counts Histogram', fontsize=14) ax3.set_xlabel('') ax3.set_ylabel('Occurrence', fontsize=14) plt.figure(figsize=(10, 10))
Eще одним тестом на нормальность распределения является Q-Q график, или график Квантиль-Квантиль. Данный график позволяет сравнить рапределение исследуемой переменной с теоретическим нормальным распределением.
Прямая красная непрерывная линия символизирует теоретическое нормальное распределение: если бы тестируемое распределение (отображается на графике круглыми точками) было нормальным, оно бы в точности легло на эту линию.
fig2, (ax1, ax2, ax3) = plt.subplots(3,1) fig2.set_size_inches(10.5, 18.5) prob1 = stats.probplot(biz_df['review_count'], dist=stats.norm, plot=ax1) ax1.set_xlabel('') ax1.set_title('Probplot against normal distribution') prob2 = stats.probplot(biz_df['rc_log'], dist=stats.norm, plot=ax2) ax2.set_xlabel('') ax2.set_title('Probplot after log transform') prob3 = stats.probplot(biz_df['rc_bc'], dist=stats.norm, plot=ax3) ax3.set_xlabel('Theoretical quantiles') ax3.set_title('Probplot after Box-Cox transform')
Борьба с выбросами (аутлаерами)
Винсоризация
Винсоризация — это серия трансформаций, направленных на ограничения влияния выбросов. 90%-ая винсоризация означает, что мы берём значения меньше 5% перцентиля и выше 95% перцентиля и приравниваем их к значениям на 5-м и 95-м перцентилях соответствиино.
import numpy as np from scipy.stats.mstats import winsorize
# пример из вики a = np.array([92, 19, 101, 58, 1053, 91, 26, 78, 10, 13, -40, 101, 86, 85, 15, 89, 89, 28, -5, 41]) winsorize(a, limits = 0.05)
101, 86, 85, 15, 89, 89, 28, -5, 41],
mask=False,
fill_value=999999)
Триминг
Триминг отличается от винсоризация тем, что мы не ограничиваем крайние значения каким-либо числом, а просто удаляем их.
from scipy.stats.mstats import trim z = [ 1, 2, 3, 4, 5, 6, 7, 8, 9,10] trim(z,(3,8))
mask=[ True, True, False, False, False, False, False, False,
True, True],
fill_value=999999)
trim(z,(0.1,0.2), relative=True)
mask=[ True, False, False, False, False, False, False, False,
True, True],
fill_value=999999)
Всякие методы, специфичные для тщательной проработки регрессионных моделей
- Bonferroni outlier test
- Hat values
- dfbetas
- Cook's distance
Шкалирование и нормализация
Шкалирование — это перевод разных признаков в одну шкалу измерений, путём деления их на некоторую константу. Некоторые признаки могут быть измерены в миллионах (например, доход), а некоторые — в очень малых величинах (например, вопросы из анкеты могут измеряться по шкале от 1 до 5). Часто такие признаки могут встречаться в одном наборе данных. В таком случае, их стоит шкалировать, что облегчить работу некоторых алгоритмов. На какие-то это почти не влияет, а, например, на KNN, очень даже влияет.
 До шкалирования
До шкалирования
Когда надо шкалировать:
- когда используется PCA, нейронные сети
- когда используются методы, основанные на подсчёте расстояний (KNN, K-means)
- когда исползуется градиентный спуск (а он сейчас используется почти везде).
Когда не обязательно:
- методы, основанные на деревьях, устойчивы на разности масштабов.
- как и линейный дискриминантный анализ или наивный байес.
Min-max scaling
Самый просто вариант — MinMax Scaling, который переносит все точки на заданный отрезок (обычно (0, 1)).
from sklearn.preprocessing import MinMaxScaler MinMaxScaler().fit_transform(data)
Стандартизация
Другая простая трансформация – это Standart Scaling (она же Z-score normalization).
Мы центрируем наш признак (среднее = 0) и шкалируем его (std = 1).
StandartScaling хоть и не делает распределение нормальным в строгом смысле слова, но в какой-то мере защищает от выбросов.
from sklearn.preprocessing import StandardScaler
-норма
Или Эвглидова нормализация. Каждый элемент вектора делится на его длинну.
from sklearn.preprocessing import normalize
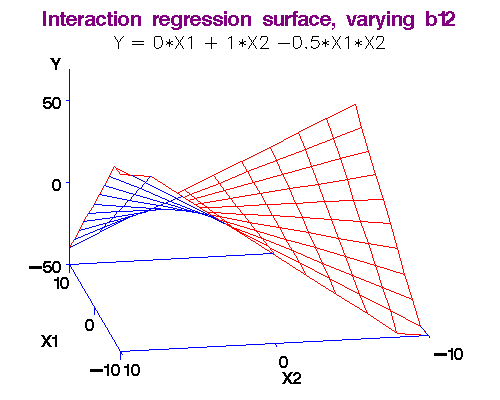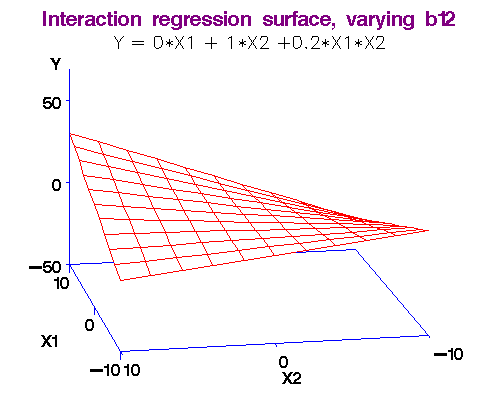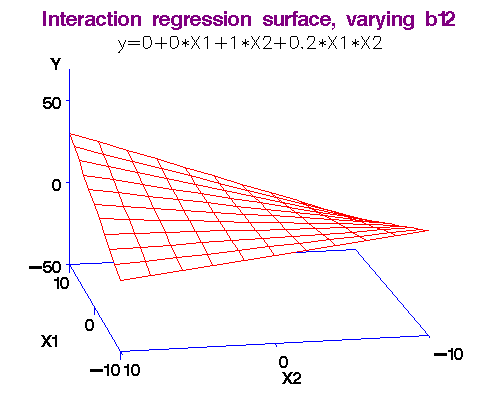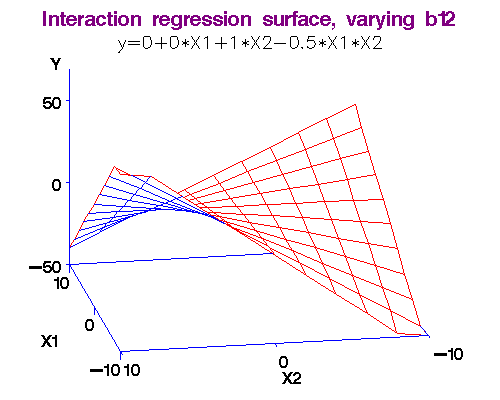
(Эффекты взаимодействия) Interaction features
Термин взаимодействие был впервые использован в работе Фишера (Fisher, 1926). "Зависит" в данном контексте не означает причинной зависимости, а просто отражает тот факт, что в зависимости от рассматриваемого подмножества наблюдений (от значения модифицирующей переменной или переменных) характер зависимости будет меняться (модифицироваться).
Признак, образованные при взаимодействии призака X и Y получается произведением этих признаков.
Полезно для многих моделей, особенно для линейных и KNN.
Трансформация категориальных признаков
Label encoding
Процесс перевода строковых фич (labels) в числовые фичи называется label encoding, т.е. мы просто присваиваем каждой категории собственный номер.
Этот метод нормально работает с методами, основанными на деревьях решений, поскольку они спообны самостоятельно разделить этот континуальный признак на сегменты, но обычно не подходит для линейных моделей.
Также Label encoding подходит для порядковых переменных, поскольку в этом случае сохраняются отношения порядка между значениями.
Frequency encoding
Вместо метки класса присваиваем частоту, с которой этот встречается. Так мы сохраним информацию о частоте каждого класса, что будет особенно полезно, если эта частота коррелирует с целевой переменной.
freq_enc = biz_df["state"].value_counts(normalize=True) biz_df["state_freq_enc"] = biz_df["state"].map(freq_enc) biz_df[["state", "state_freq_enc"]].head(6)
| state | state_freq_enc | |
|---|---|---|
| 0 | AZ | 0.999740 |
| 1 | AZ | 0.999740 |
| 2 | AZ | 0.999740 |
| 3 | AZ | 0.999740 |
| 4 | AZ | 0.999740 |
| 5 | CA | 0.000087 |
One-hot encoding
- Шкалирование происходит автоматически
- Сильно разрастается размер матрицы
- Если у вас много one-hot encoded признаков и несклько метрических, то деревья решений могут испытывать сложности с тем, что использовать метрические признаки эффективно.
pd.get_dummies(biz_df["state"]).head()
| AZ | CA | CO | SC | |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 |
Feature hashing
Mean encoding
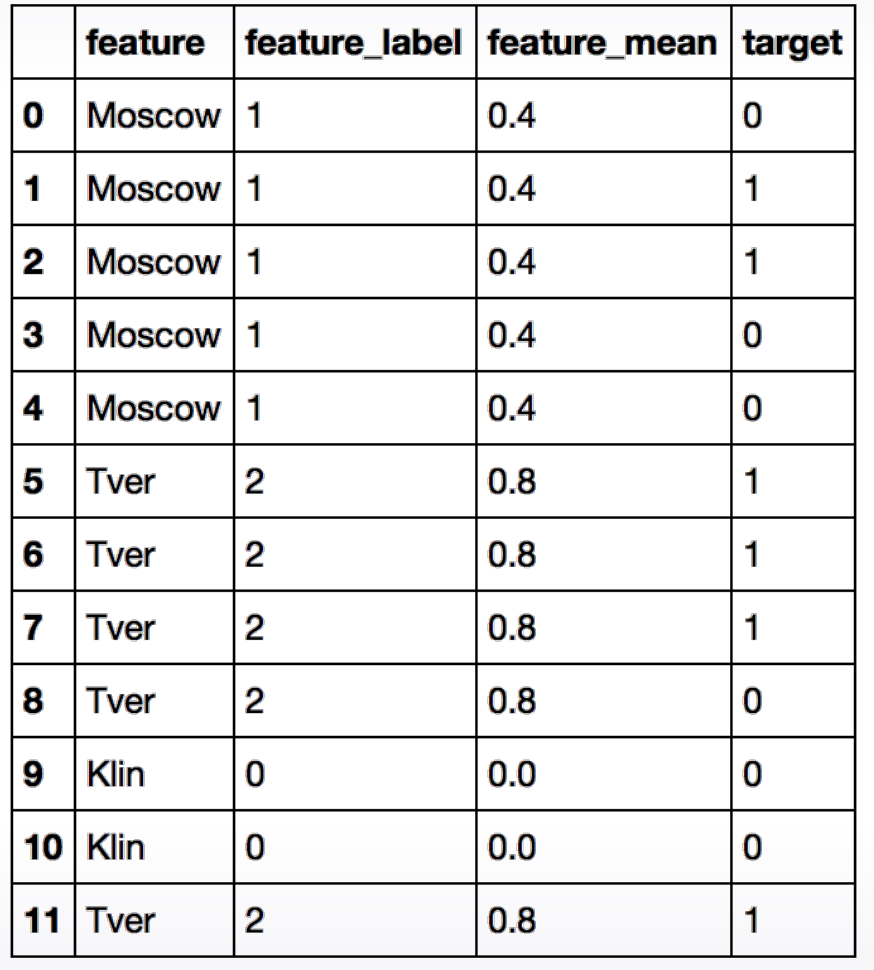
Подходит для бинарной классификации. Кодируем категориальную переменную на основе доли положительного класса в каждой категории. Самостоятельно можно реализовать этот метод примерно таким образом:
import pandas as pd df_tr = pd.read_csv("https://gist.github.com/michhar/2dfd2de0d4f8727f873422c5d959fff5/raw/ff414a1bcfcba32481e4d4e8db578e55872a2ca1/titanic.csv", sep='\t') col = "Pclass" cumsum = df_tr.groupby("Pclass")["Survived"].cumsum() - df_tr["Survived"] cumcount = df_tr.groupby("Pclass").cumcount() df_tr["cumsum"] = cumsum df_tr["cumcount"] = cumcount df_tr["Pclass_mean_target"] = cumsum/cumcount df_tr[["Pclass", "cumsum", "cumcount", "Pclass_mean_target", "Survived"]].head(10)
| Pclass | cumsum | cumcount | Pclass_mean_target | Survived | |
|---|---|---|---|---|---|
| 0 | 3 | 0 | 0 | NaN | 0 |
| 1 | 1 | 0 | 0 | NaN | 1 |
| 2 | 3 | 0 | 1 | 0.000000 | 1 |
| 3 | 1 | 1 | 1 | 1.000000 | 1 |
| 4 | 3 | 1 | 2 | 0.500000 | 0 |
| 5 | 3 | 1 | 3 | 0.333333 | 0 |
| 6 | 1 | 2 | 2 | 1.000000 | 0 |
| 7 | 3 | 1 | 4 | 0.250000 | 0 |
| 8 | 3 | 1 | 5 | 0.200000 | 1 |
| 9 | 2 | 0 | 0 | NaN | 1 |
Модели, основанные на этом подходе могут переобучаться. Есть разные стратегии борьбы с переобучением:
- Кросс-валидация. Считаем среднее на одной выборке, добавляем их в другую.
- Сглаживание. , где задаёт силу регуляризации.
- Добавление шума.
- Expanding mean 👑. Лучший способ, используется в CatBoost.
Работа с пропущенными значениями
Вначале надо понять, как они закодированы. Не всего это стандартный NaN, это может быть -999, "", -1 и др. в зависимости от данных.
После идентификации пропущенных значений, надо решить, что с ними делать. Основные подходы следующие:
- Удалить строки с пропущенными значениями. Слишком большая роскошь.
- Присовить пропущенным значениям некоторое другое значение, которое не встречалось преже. Тем самым мы создадим отдельную категорию «пропущенные значения». Это не очень работает для линейных моделей и нейронных сетей.
- Присовить пропущенным значениям среднее, медиану или самое часто стречающееся значение. Хорошо работает для линейных моделей и нейронных сетей, но так себе для деревьев.
- Постараться как-нибудь хитро реконструировать пропущенные значения. Это всегда возможно, если мы имеем дело с последовательностями, например временными.
Feature extraction
Выбор важных признаков (feature selection)
- Irrelevant Features and the Subset Selection Problem
- Curse of dimensionality
- An Introduction to Feature Selection
- Beginner's Guide to Feature Selection in Python
Хорошо, допустим, мы создали много, очень много новых фич. Что дальше?
А дальше надо отобрать наиболее информативные из них. Отбор фич полезен по следующим причинам:
- Увеличивается скорость обучения модели.
- Увеличивается интерпретируемость модели.
- Уменьшается риск пререобучения модели.
- Увеличивается точность модели.
- Помогает ослабить «проклятие размерности».
Существует по меньшей мере четыре способа отбора наиболее важных признаков.
Фильтрация
Applying Filter Methods in Python for Feature Selection
Отфильтровываем безполезные для модели признаки. Например, те, которые сильно скоррелированы или те, которые не нужны. Пример — удаление стоп слов в обработке естестенного языка.
Это техики незатратные по времени выполнения, но они не принимают во внимание модель, поэтому есть риск удалить нужное.
Они основаны на статистических методах и, как правило, рассматривают каждую фичу независимо. Позволяют оценить и ранжировать фичи по значимости, за которую принимается степень корреляции этой фичи с целевой переменной.
Плюсы
- Низкая стоимость вычислений, которая зависит линейно от общего количества фич. Они значительно быстрее и wrapper и embedded методов.
- Хорошо работают даже тогда, когда число фич у нас превышает количество примеров в тренировочном сете (чем далеко не всегда могут похвастаться методы других категорий).
Минусы
- Не принимают во внимание модель, поэтому есть риск удалить нужное. Найти топ-N наиболее коррелирующих признаков вообще говоря не означает получить подмножество, на котором точность предсказания будет наивысшей.
Univariate Filter Methods
Самый очевидный кандидат на отстрел – признак, у которого значение неизменно, т.е. не содержит вообще никакой информации. Если немного отойти от этого вырожденного случая, резонно предположить, что низковариативные признаки скорее хуже, чем высоковариативные. Так можно придти к идее отсекать признаки, дисперсия которых ниже определенной границы.
from sklearn.feature_selection import VarianceThreshold
Есть и другие способы, основанные на Informaition gain, chi-square test, mRmR.
Wrapper methods
Applying Wrapper Methods in Python for Feature Selection
Суть этой категории методов в том, что классификатор запускается на разных подмножествах фич исходного тренировочного сета. После чего выбирается подмножество фич с наилучшими параметрами на обучающей выборке. А затем он тестируется на тестовом сете (тестовый сет не участвует в процессе выбора оптимального подмножества).
Плюсы
- Поскольку одновременно оценивается выборка фич, можно выявлять возможные взаимодействия между ними.
- Позволяет найти сочетание признаков, которое лучше всего работает для конкретного алгоритма.
Минусы
- Высокий риск переобучения, когда количество наблюдений недостаточно.
- Более ресурсоёмкий метод, чем фильтрация.

Виды
Есть три подхода в этом классе методов — методы включения (forward selection), исключения (backwards selection) фич и исчерпывающий метод (exhaustive feature selection).
В методах включения на первом этапе производительность классификатора оценивается на каждом признаке. Признак, которая показывает наилучшие результаты, выбирается из всех признаком. На втором этапе эффективность первого признака проверяется в сочетании со всеми другими признаками. Выбирается комбинация двух признаком, обеспечивающих наилучшую производительность алгоритма. Процесс продолжается до тех пор, пока не будет выбрано определённое количество признаков.
Методы выключения начинают с подмножества равного исходному множеству фич, и из него постепенно удаляются фичи, с пересчетом классификатора каждый раз.
Реализация методов включения и выключения доступна в библиотеке mlxtend.
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier from sklearn.metrics import roc_auc_score from mlxtend.feature_selection import SequentialFeatureSelector feature_selector = SequentialFeatureSelector(RandomForestClassifier(n_jobs=-1), k_features=15, forward=True, verbose=2, scoring='roc_auc', cv=4)
При исчерпывающем выборе принзаков качество работы алгоритма машинного обучения оценивается по всем возможным сочетаниям признаков в наборе данных. Выбирается подмножество функций, обеспечивающее наилучшую производительность. Исчерпывающий алгоритм поиска является наиболее ресурсозатратным алгоритмом всех wrapper methods.
Пример использования метода исчерпывающего выбора из библиотеки mlxtend:
from mlxtend.feature_selection import ExhaustiveFeatureSelector from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier from sklearn.metrics import roc_auc_score feature_selector = ExhaustiveFeatureSelector(RandomForestClassifier(n_jobs=-1), min_features=2, max_features=4, scoring='roc_auc', print_progress=True, cv=2)
Embedded methods
Встроенные методы позволяют не разделять отбор фич и обучение классификатора, а производят отбор внутри процесса расчета модели. К тому же эти алгоритмы требуют меньше вычислений, чем wrapper methods (хотя и больше, чем методы фильтрации).
Основным методом из этой категории является регуляризация. Существуют различные ее разновидности, но основной принцип общий. Если рассмотреть работу классификатора без регуляризации, то она состоит в построении такой модели, которая наилучшим образом настроилась бы на предсказание всех точек тренировочного сета. Идея регуляризации в том, чтобы построить алгоритм минимизирующий не только ошибку, но и количество используемых переменных.
Отбор с использованием моделей
Другой подход: использовать какую-то baseline модель для оценки признаков, при этом модель должна явно показывать важность использованных признаков. Обычно используются два типа моделей: какая-нибудь "деревянная" композиция (например, Random Forest) или линейная модель с Lasso регуляризацией, склонной обнулять веса слабых признаков. Логика интутивно понятна: если признаки явно бесполезны в простой модели, то не надо тянуть их и в более сложную.
Автоматическое конструирование признаков при помощи Deep Feature Synthesis
- Deep Feature Synthesis: Towards Automating Data Science Endeavors
- Automated Feature Engineering in Python
- Why Automated Feature Engineering Will Change the Way You Do Machine Learning
- Automated Feature Engineering in Python
- Introduction to Automated Feature Engineering Using Deep Feature Synthesis (DFS)
- Machine Learning with Kaggle: Feature Engineering
An open source python framework for automated feature engineering
DFS - это метод автоматического извлечения признаков из реляционных данных. DFS совмещает несколько базовых функций аггрегации и трансформации, чтобы получить новый признак.
Глубина признака - это просто количество функций, необходимых для создания признака. Признак, которая создан при помощи одного преобразования, будет иметь глубину 1 и т.д.
Работа со специфическими данными
Текст
Это мы проходили, так что вы мне и скажите:
- В чем проблема извлечения признаков из текстовых данных?
- Какие специфические этапы трансформации признаков существуют при работе с текстами?
Время
tsfresh — библиотека для автоматической генерации признаков из временных рядов
- количество времени прошеднего с/до определенного момента, например праздников.
- выделение сезонов, времен года, кварталов, дней недели
- разделение времени на часы, минуты и секунды
- преобразование времени в радиальную ситему координат.
Географические координаты
Подумаем сами.
Изображения
Раньше существовало множество методов выделения признаков из изображений, а сейчас все в основном используют CNN.
Самостоятельное задание
Займите место >=15 в соревновании и получите автомат за курс. Займите 1 место и получите 400 000₽ впридачу.
Набор данных с соревнования (не все данные).

Комментарии