Основны машинного обучения и линейной регресси в Python
При подготовке использовались следующие материалы:
- Открытый курс машинного обучения. Тема 4. Линейные модели классификации и регрессии.
- Базовые принципы машинного обучения на примере линейной регрессии.
- Материалы курсы «Машинное обучение» на ФКН ВШЭ.
- Python Machine Learning: Machine Learning and Deep Learning with Python, scikit-learn, and TensorFlow, 2nd Edition by Sebastian Raschka.
- A Course of Econometrics by D.S.G. Pollock
- и многие другие...
Машинное обучение — это подраздел искусственного интеллекта, в котором изучаются алгоритмы, способные обучаться без прямого программирования того, что нужно изучать.
Говорят, что программа обучается на опыте E относительно класса задач T в смысле меры качества L, если при решении задачи T качество, измеряемое мерой L, возрастает при демонстрации нового опыта E.
У нас есть задача, данные и способ оценки программы/модели. Давайте определим, что такое модель, и что значит обучить модель. Предиктивная модель – это параметрическое семейство функций (семейство гипотез): \Large \mathcal{H} = \left{ h\left(x, \theta\right) | \theta \in \Theta \right} где
- — множество параметров
Таким образом, из большого семейства гипотез мы должны выбрать какую-то одну конкретную, которая с точки зрения меры является лучшей. Процесс такого выбора назовем алгоритмом обучения.
Получается, что алгоритм обучения — это отображение из набора данных в пространство гипотез. Обычно процесс обучения с учителем состоит из двух шагов:
- обучение: ;
- применение: .
Вводится функционал качества, характеризующий среднюю ошибку (эмпирический риск) алгоритма на произвольной выборке. В вероятностном подходе в роли функционала качества обычно рассматривается математическое ожидание функции потерь, называемое риском. Риск характеризует среднее качество алгоритма (решающей функции) на генеральной совокупности.
Часто для обучения модели пользуются принципом минимизации эмпирического риска. Эмпирический риск (Empirical Risk) — это средняя величина ошибки алгоритма на обучающей выборке. Для рассчёта эмпирического риска вводятся:
- Функция потерь , характеризующая величину отклонения ответа от правильного ответа на произвольном объекте .
- Модель зависимости , в рамках которой будет вестись поиск отображения, приближающего неизвестную целевую зависимость.
У данного принципа есть существенный недостаток, решения найденные таким путем будут склонны к переобучению. Мы говорим, что модель обладает обобщающей способностью, тогда, когда ошибка на новом (тестовом) наборе данных (взятом из того же распределения мала, или же предсказуема. Переобученная модель не обладает обобщающей способностью, т.е. на обучающем наборе данных ошибка мала, а на тестовом наборе данных ошибка существенно больше.
Обучение с учителем
Обучение с учителем (Supervised learning) — один из разделов машинного обучения, посвященный решению следующей задачи. Имеется множество объектов (ситуаций) и множество возможных ответов (откликов, реакций). Существует некоторая зависимость между ответами и объектами, но она неизвестна. Известна только конечная совокупность прецедентов — пар «объект, ответ», называемая обучающей выборкой. На основе этих данных требуется восстановить зависимость, то есть построить алгоритм, способный для любого объекта выдать достаточно точный ответ. Для измерения точности ответов определённым образом вводится функционал качества. Под учителем понимается либо сама обучающая выборка, либо тот, кто указал на заданных объектах правильные ответы.
Как правило, в задачах обучения с учителем, опыт E представляется в виде множества пар признаков и целевых переменных: D=\left{ (x_i, y_i) \right}_{i=1, \ldots,n}
Регрессия
Предсказание количественного признака объекта.
Классификация
Предсказание категориального признака объекта.
Обучение без учителя
Обучение без учителя (Unsupervised learning) — один из разделов машинного обучения. Изучает широкий класс задач обработки данных, в которых известны только описания множества объектов (обучающей выборки), и требуется обнаружить внутренние взаимосвязи, зависимости, закономерности, существующие между объектами.
Кластеризация
Кластеризация — задача разделения объектов на группы, обладающие неко- торыми свойствами. Примером может служить кластеризация документов из электронной библиотеки или кластеризация абонентов мобильного оператора.
Оценивание плотности
Оценивание плотности — задача приближения распределения объектов. При- мером может служить задача обнаружения аномалий, в которой на этапе обу- чения известны лишь примеры «правильного» поведения оборудования (или, скажем, игроков на бирже), а в дальнейшем требуется обнаруживать случаи некорректной работы (соответственно, незаконного поведения игроков). В та- ких задачах сначала оценивается распределение «правильных» объектов, а за- тем аномальными объявляются все объекты, которых в рамках этого распре- деления получают слишком низкую вероятность.
Визуализация
Визуализация — задача изображения многомерных объектов в двумерном или трехмерном пространстве таким образом, что сохранялось как можно больше зависимостей и отношений между ними.
Понижение размерности
Понижение размерности — задача генерации таких новых признаков, что их меньше, чем исходных, но при этом с их помощью задача решается не хуже (или с небольшими потерями качества, или лучше — зависит от постановки). К этой же категории относится задача построения латентных моделей, где требуется описать процесс генерации данных с помощью некоторого (как правило, неболь- шого) набора скрытых переменных. Примерами являются задачи тематическо- го моделирования и построения рекомендаций, которым будет посвящена часть курса.
Частичное обучение
Частичное обучение (semi-supervised lerning) — один из методов машинного обучения, использующий при обучении как размеченные, так и неразмеченные данные. Обычно используется небольшое количество размеченных и значительный объём неразмеченных данных. Частичное обучение является компромисом между обучением без учителя (без каких-либо размеченных обучающих данных) и обучением с учителем (с полностью размеченным набором обучения). Было замечено, что неразмеченные данные, будучи использованными совместно с небольшим количеством размеченных данных, могут обеспечить значительный прирост качества обучения.
Обучение с подкреплением
Испытуемая система (агент) обучается, взаимодействуя с некоторой средой. Откликом среды (а не специальной системы управления подкреплением, как это происходит в обучении с учителем) на принятые решения являются сигналы подкрепления, поэтому такое обучение является частным случаем обучения с учителем, но учителем является среда или её модель.
Идея обучения с подкреплением была почерпнута в смежной области психологии. В терминах психологии ОСП изучает, как агент должен действовать в окружении, чтобы максимизировать некоторый долговременный выигрыш. Алгоритмы с частичным обучением пытаются найти стратегию, приписывающую состояниям окружающей среды действия, которые должен предпринять агент в этих состояниях. В экономике и теории игр обучение с подкреплением рассматривается в качестве интерпретации того, как может установиться равновесие.
Теория регрессионного анализа
Модель из категории «обучение с учителем», устанавливающая связь между одним или несколькими независимыми признааками (предикторами) и завсимыми континуальным призаком.
Линейная регрессия
В линейной регрессии моделью зависимости является формула прямой линии.
Простая линейная регрессия
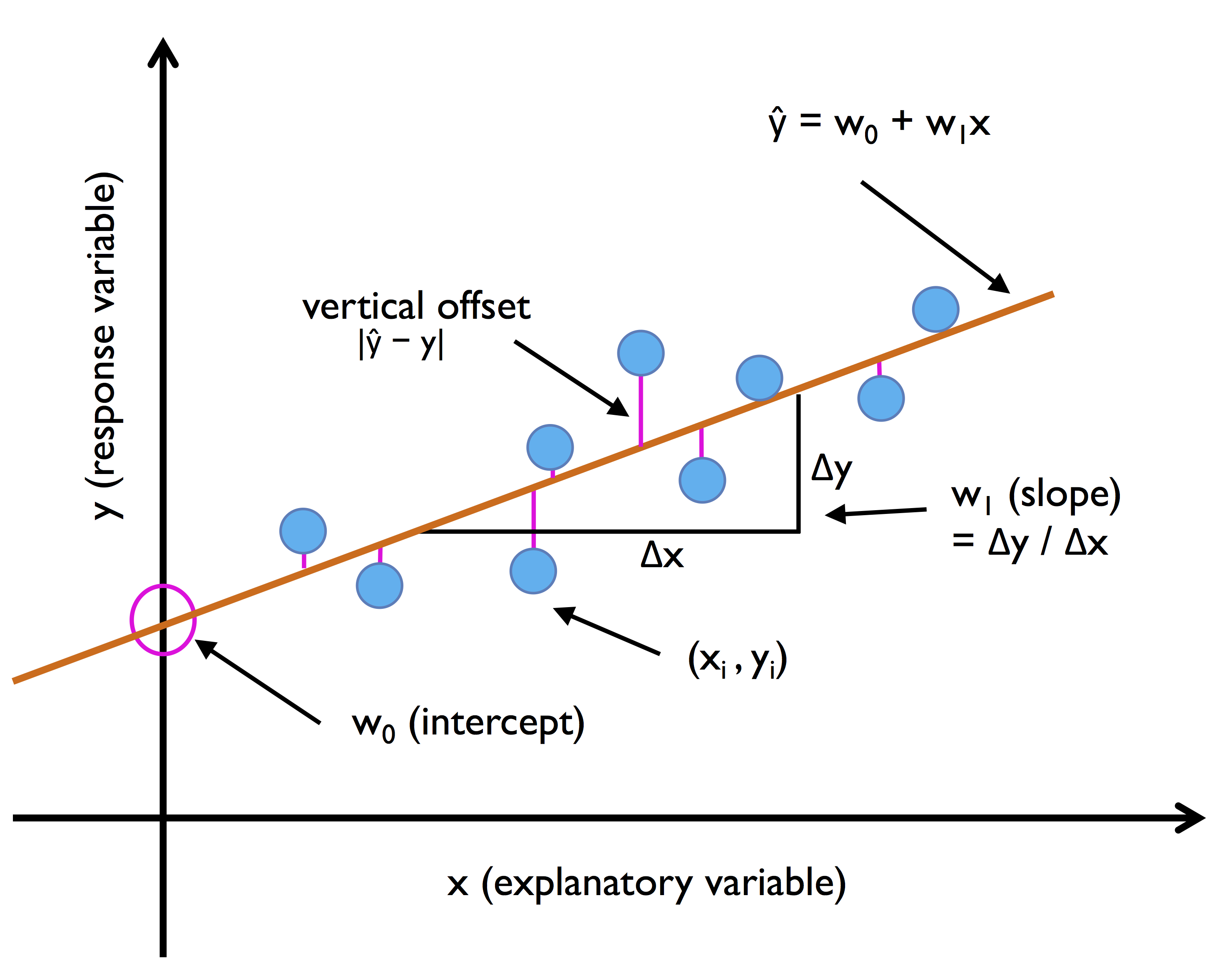
Простая (одномерная) линейная регрессия (модель с одним предиктором) аппроксимируется всем известной со школы функцией прямой линии с той лишь разницей, что теперь нужно добавить случайную ошибку : где
- — зависимая переменная (отклик)
- — известная константа (значение объясняющей переменной, измерянной в i-ом эксперименте)
- , — параметры модели (свободный член и угловой коэффициент).
- — случайная ошибка
Графически она выглядит следующим образом:
Множественная линейная регрессия
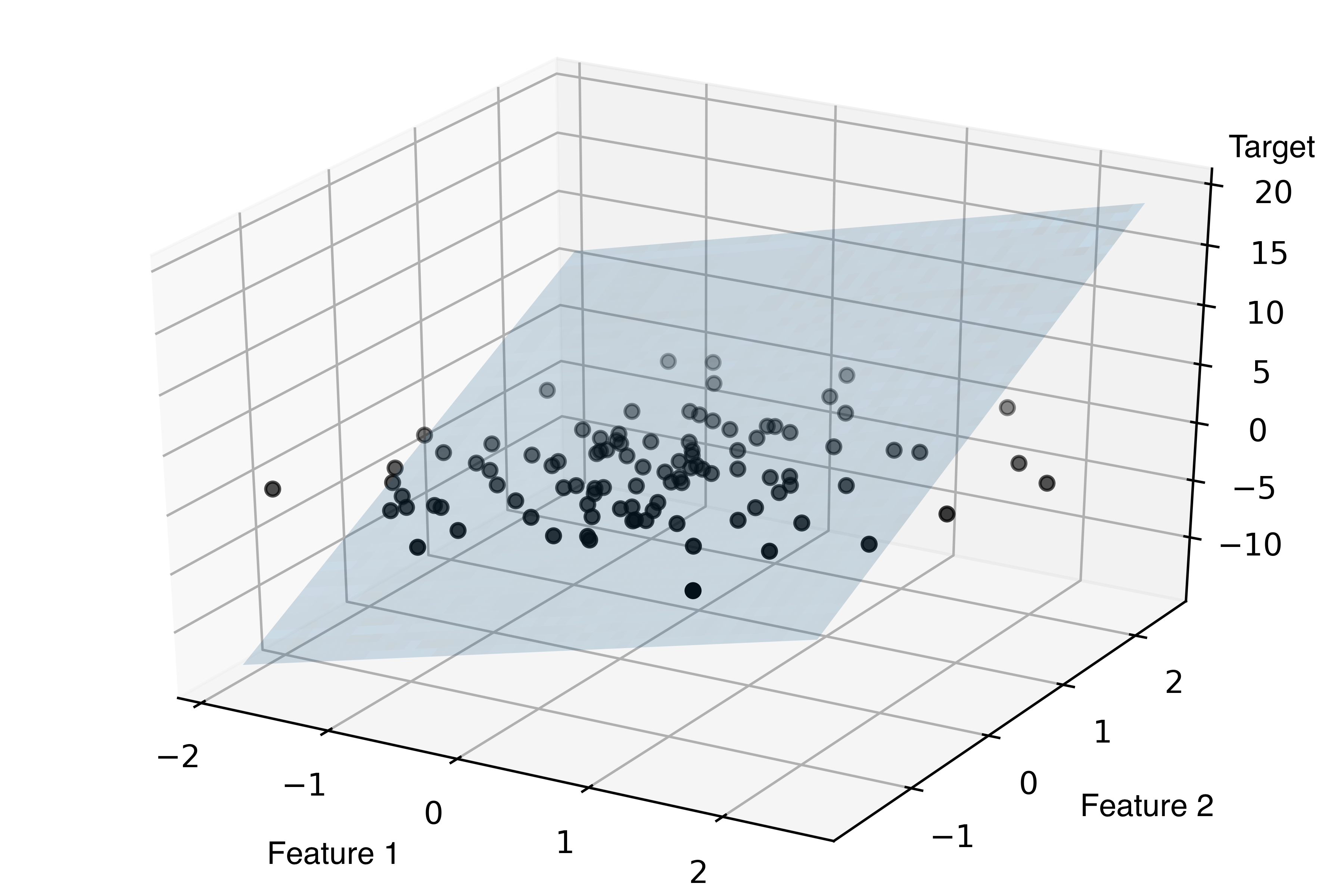
Для простоты примем, что . Тогда в общем случае форма линейной регрессии выглядит следующим образом:
Пример графика для линейной регрессионной модели с двумя независимыми переменными:
Метрики качества регрессионной модели
Итак, у нас имеет модель
Существует несколько методов для оценки регрессионной модели:
Средняя абсолютная ошибка (MAE) — это просто усреднённое значение модулей ошибок:
Модуль отклонения не является дифференцируемым, но при этом менее чувствителен к выбросам, чем квадрат отклонения MSE.
Средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE)
Среднеквадратическая ошибка (MSE). Для вычисления среднеквадратической ошибки все отдельные остатки регрессии возводятся в квадрат, суммируются, сумма делится на общее число ошибок:
Благодаря своей дифференцируемости эта функция наиболее часто используется в задачах регрессии.
Квадрат отклонения делает особый акцент на объектах с сильной ошибкой, и метод обучения будет в первую очередь стараться уменьшить отклонения на таких объектах. Если же эти объекты являются выбросами (то есть значение целевой переменной на них либо ошибочно, либо относится к другому распределению и должно быть проигнорировано), то такая расстановка акцентов приведёт к плохому качеству модели. Модуль отклонения (MAE) в этом смысле гораздо более терпим к сильным ошибкам.
Величина среднеквадратичного отклонения плохо интерпретируется, поскольку не сохраняет единицы измерения — так, если мы предсказываем цену в рублях, то MSE будет измеряться в квадратах рублей. Чтобы избежать этого, используют корень из среднеквадратичной ошибки.
Корень из среднеквадратической ошибки (RMSE):
Эти метрики хорошо подходят для сравнения двух моделей или для контроля качества во время обучения, но не позволяют сделать выводы том, насколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации (или коэффициент )
Так же все эти метрики можно отнести к функциям потерь, поскольку мы хотим их минимизировать.
Функция потерь — функция, которая в теории статистических решений характеризует потери при неправильном принятии решений на основе наблюдаемых данных. Если решается задача оценки параметра сигнала на фоне помех, то функция потерь является мерой расхождения между истинным значением оцениваемого параметра и оценкой параметра.
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объяснённую моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Другими словами

Среднеквадратичная логарифмическая ошибка (mean squared logarithmic error, MSLE) Данная метрика подходит для задач с неотрицательной целевой переменной. За счёт логарифмирования ответов и прогнозов мы скорее штрафуем за отклонения в порядке величин, чем за отклонения в их значениях. Также следует помнить, что логарифм не является симметричной функцией, и поэтому данная функция потерь штрафует заниженные прогнозы сильнее, чем завышенные.
Осторожно! Не всегда можно полагаться на цифры. Если это возможно, лучше также построить график зависимости от . Это позволит Вам избежать попадания в ловушку квадрата Энскомба. Основные числовые характеристики этих данных идентичны и все эти зависимости описываются формулой , но, очевидно, выглядят они по-разному:

Обучение линейной регрессии
Метод наименьших квадратов
Чаще всего линейная регрессия обучается с использованием среднеквадратичной ошибки. В этом случае получаем задачу оптимизации функции стоимости (эмпирического риска) (считаем, что среди признаков есть константный, и поэтому свободный коэффициент не нужен). Оценка МНК является лучшей оценкой параметров модели, среди всех линейных и несмещенных оценок, то есть обладающей наименьшей дисперсией (из теоремы Гаусса — Маркова).
Недостатки метода наименьших квадратов Наличие явной формулы для оптимального вектора весов — это большое преимущество линейной регрессии. Но аналитическое решение не всегда возможно по ряду причин:
- Обращение матрицы — сложная операция с кубической сложностью от количества признаков. Если в выборке тысячи признаков, то вычисления могут стать слишком трудоёмкими. Решить эту проблему можно путём использования численных методов оптимизации.
- Матрица может быть вырожденной (определитель равено 0 → нет обратной матрицы) или плохо обусловленной. В этом случае обращение либо невозможно, либо может привести к неустойчивым результатам. Проблема решается с помощью регуляризации.
Ограничения линейной регрессии
- Линейность: зависимая переменная может линейно аппроксимировать независимые переменные
- Нормальность распределения Y и ε
- Отсутствие избытка влиятельных наблюдений
- Гомоскадастичность распределения остатков
- Отсутсвие мультиколлинеарности
Не все эти ограничения должны соблюдаться на 100%, особенно, если Вы занимаетес машинным обучением.
Практическое занятие с Housing Dataset
Применим полученные навыки для анализа данных о ценах на недвижимость в Бостоне, опубликованных в статье 1978 г.
import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns %matplotlib inline df = pd.read_csv("housing.txt", header=None, sep='\s+') df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV'] df.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | MEDV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
Ещё данные можно подгрузить из втроенной в sklearn коллекции:
from sklearn.datasets import load_boston boston = load_boston() print(boston.DESCR) df = pd.DataFrame(boston.data, columns=boston.feature_names) df['MEDV'] = boston.target df.head()
===========================
Notes
------
Data Set Characteristics:
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive
:Median Value (attribute 14) is usually the target
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
http://archive.ics.uci.edu/ml/datasets/Housing
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
**References**
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
- many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | MEDV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
Разведывательный анализ
Как всегда начинаем изучение нового набора данных с разглядывания графиков, показывающих распределение переменных.
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV'] sns.pairplot(df[cols], size=2.5)
warnings.warn(msg, UserWarning)
Визуализируем матрицу корреляций и ввиде тепловой карты:
sns.set(font_scale=1.5) hm = sns.heatmap(df[cols].corr(), cbar=True, annot=True)
Регрессионный анализ
Приступим к построению регрессионной модели. Определим зависимые и независимые переменные:
X = df[['LSTAT']].values y = df['MEDV'].values
from sklearn.linear_model import LinearRegression slr = LinearRegression() slr.fit(X, y) y_pred = slr.predict(X) print('Slope: {:.2f}'.format(slr.coef_[0])) print('Intercept: {:.2f}'.format(slr.intercept_))
Intercept: 34.55
linalg.lstsq(X, y)
PS: эти непонятные символы в фигурных скобках задают вид форматирования строки. В данном случае мы говорим, что хотим вывести число с плавающей точкой с точностью до двух знаков. Подробнее в Format Specification Mini-Language.
plt.scatter(X, y) plt.plot(X, slr.predict(X), color='red', linewidth=2)
Для быстрой визуализации линейной зависимости можно также использовать функцию regplot из seaborn.
sns.regplot(x="LSTAT", y="MEDV", data=df)
return np.add.reduce(sorted[indexer] * weights, axis=axis) / sumval
Проверка качество модели: практика
Возможные метрики для проверки качества модели в sklearn можно посмотреть в документации, а можно посчитать самим по формулам. Выберем простой путь.
from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values y = df['MEDV'].values X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.3, random_state=0)
slr = LinearRegression() slr.fit(X_train, y_train) y_train_pred = slr.predict(X_train) y_test_pred = slr.predict(X_test)
Поскольку в нашей модели обычно несколько независимых переменных, мы не можем отобразить их зависимость на двумерном пространстве, но можем нанести на график связь между остатками модели и предсказанными значениями, что также поможет нам диагностировать качество модели. Это называется Residuals plot. C его помощью мы можем увидет нелинейность и выбросы, проверить случайность распределения ошибки.
plt.scatter(y_train_pred, y_train_pred - y_train, c='blue', marker='o', label='Training data') plt.scatter(y_test_pred, y_test_pred - y_test, c='lightgreen', marker='s', label='Test data') plt.xlabel('Predicted values') plt.ylabel('Residuals') plt.legend(loc='upper left') plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='red') plt.xlim([-10, 50]) plt.tight_layout()
from sklearn.metrics import mean_absolute_error, mean_squared_error, median_absolute_error, r2_score print('MSE train: {:.3f}, test: {:.3f}'.format( mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred))) print('R^2 train: {:.3f}, test: {:.3f}'.format( r2_score(y_train, y_train_pred), r2_score(y_test, y_test_pred)))
R^2 train: 0.764, test: 0.674
Другой взгляд на построение статистических моделей — statsmodels
Statsmodels — ещё одна библиотека для построения статистических данных в Python, но выполненная в лучших традийиях R. Посмотрим, сравним реализацию линейных моделей в sklearn и statsmodels.
from sklearn.linear_model import LinearRegression X = df[['LSTAT']].values y = df['MEDV'].values slr = LinearRegression() slr.fit(X, y) y_pred = slr.predict(X) print('Slope: {:.2f}'.format(slr.coef_[0])) print('Intercept: {:.2f}'.format(slr.intercept_))
Intercept: 34.55
import statsmodels.api as sm import statsmodels.formula.api as smf results = smf.ols('MEDV ~ LSTAT', data=df).fit() results.summary()
Использование категориальных переменных в качестве предикторов
Label Encoding
Самый простой и очевидный способ перекодировки — просто заменить строки на числа. В модуле preprocessing библиотеки sklearn именно для этой задачи реализован класс LabelEncoder.
from sklearn import preprocessing le = preprocessing.LabelEncoder() le.fit(["paris", "paris", "tokyo", "amsterdam"]) le.transform(["tokyo", "tokyo", "paris"])
Метод fit этого класса находит все уникальные значения и строит таблицу для соответствия каждой категории некоторому числу, а метод transform непосредственно преобразует значения в числа. После fit у label_encoder будет доступно поле classes_, содержащее все уникальные значения. Можно их пронумеровать и убедиться, что преобразование выполнено верно.
При использовании этого подхода мы всегда должны быть уверены, что признак не может принимать неизвестных ранее значений, иначе вылезет ошибка.
Однако, такое представление имеет мало смысла и, более того, не корректно, поскольку таким образом мы определяем для этой переменной недопустимые математические операции.
One-Hot Encoding
Предположим, что некоторый признак может принимать 10 разных значений. В этом случае One Hot Encoding подразумевает создание 10 признаков, все из которых равны нулю за исключением одного. На позицию, соответствующую численному значению признака мы помещаем 1.
Эта техника реализована в sklearn.preprocessing в классе OneHotEncoder. По умолчанию OneHotEncoder преобразует данные в разреженную матрицу, чтобы не расходовать память на хранение многочисленных нулей. Однако в этом примере размер данных не является для нас проблемой, поэтому мы будем использовать "плотное" представление.
cars_df = pd.DataFrame({ "car": ["BMW", "Audi", "BMW", "Mersedes"], "retailer": ["Best cars ever", "Best cars ever", "Best cars ever", "AutoMoto"] }) cars_df
| car | retailer | |
|---|---|---|
| 0 | BMW | Best cars ever |
| 1 | Audi | Best cars ever |
| 2 | BMW | Best cars ever |
| 3 | Mersedes | AutoMoto |
pd.get_dummies(cars_df)
| car_Audi | car_BMW | car_Mersedes | retailer_AutoMoto | retailer_Best cars ever | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 |
Можно использовать модуль OneHotEncoder из SkLearn, но с ним не так всё просто — необходимо сначала преобразовать значения в числа как в label encoding. Проще использовать LabelBinarizer:
from sklearn import preprocessing lb = preprocessing.LabelBinarizer() lb.fit_transform(cars_df["car"])
[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
Пример работы с категориальными данными
Пусть это будут данные о престиже различных профессий в США.
import statsmodels.api as sm import statsmodels.formula.api as smf duncan_prestige = sm.datasets.get_rdataset("Duncan", "car")
print(duncan_prestige.__doc__)
| Duncan | R Documentation |
+----------+-------------------+
Duncan's Occupational Prestige Data
-----------------------------------
Description
~~~~~~~~~~~
The ``Duncan`` data frame has 45 rows and 4 columns. Data on the
prestige and other characteristics of 45 U. S. occupations in 1950.
Usage
~~~~~
::
Duncan
Format
~~~~~~
This data frame contains the following columns:
type
Type of occupation. A factor with the following levels: ``prof``,
professional and managerial; ``wc``, white-collar; ``bc``,
blue-collar.
income
Percent of males in occupation earning $3500 or more in 1950.
education
Percent of males in occupation in 1950 who were high-school
graduates.
prestige
Percent of raters in NORC study rating occupation as excellent or
good in prestige.
Source
~~~~~~
Duncan, O. D. (1961) A socioeconomic index for all occupations. In
Reiss, A. J., Jr. (Ed.) *Occupations and Social Status.* Free Press
[Table VI-1].
References
~~~~~~~~~~
Fox, J. (2008) *Applied Regression Analysis and Generalized Linear
Models*, Second Edition. Sage.
Fox, J. and Weisberg, S. (2011) *An R Companion to Applied Regression*,
Second Edition, Sage.
duncan_prestige.data.head(5)
| type | income | education | prestige | |
|---|---|---|---|---|
| accountant | prof | 62 | 86 | 82 |
| pilot | prof | 72 | 76 | 83 |
| architect | prof | 75 | 92 | 90 |
| author | prof | 55 | 90 | 76 |
| chemist | prof | 64 | 86 | 90 |
prestige_df = duncan_prestige.data.copy() prestige_dummies = pd.get_dummies(prestige_df.select_dtypes(include=[object])) prestige_df = pd.concat([prestige_df, prestige_dummies], axis=1)
prestige_df.head()
| type | income | education | prestige | type_bc | type_prof | type_wc | |
|---|---|---|---|---|---|---|---|
| accountant | prof | 62 | 86 | 82 | 0 | 1 | 0 |
| pilot | prof | 72 | 76 | 83 | 0 | 1 | 0 |
| architect | prof | 75 | 92 | 90 | 0 | 1 | 0 |
| author | prof | 55 | 90 | 76 | 0 | 1 | 0 |
| chemist | prof | 64 | 86 | 90 | 0 | 1 | 0 |
from sklearn.linear_model import LinearRegression X_prestige = prestige_df.drop(["type", "prestige"], axis=1).values y_prestige = prestige_df['prestige'].values X_train_prestige, X_test_prestige, y_train_prestige, y_test_prestige = train_test_split( X_prestige, y_prestige, test_size=0.3, random_state=0) slr_prestige = LinearRegression() slr_prestige.fit(X_train_prestige, y_train_prestige) y_train_pred = slr_prestige.predict(X_train_prestige) y_test_pred = slr_prestige.predict(X_test_prestige) print('Slope: {}'.format(slr_prestige.coef_)) print('Intercept: {:.2f}'.format(slr_prestige.intercept_))
Intercept: 2.74
Похожую вещь можно сделать с помощью statsmodels, и про том гораздо проще:
results = smf.ols('prestige ~ education + income + C(type)', data=prestige_df).fit()
results.summary()
| Dep. Variable: | prestige | R-squared: | 0.913 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.904 |
| Method: | Least Squares | F-statistic: | 105.0 |
| Date: | Fri, 03 Nov 2017 | Prob (F-statistic): | 1.17e-20 |
| Time: | 14:56:00 | Log-Likelihood: | -163.65 |
| No. Observations: | 45 | AIC: | 337.3 |
| Df Residuals: | 40 | BIC: | 346.3 |
| Df Model: | 4 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -0.1850 | 3.714 | -0.050 | 0.961 | -7.691 | 7.321 |
| C(type)[T.prof] | 16.6575 | 6.993 | 2.382 | 0.022 | 2.524 | 30.791 |
| C(type)[T.wc] | -14.6611 | 6.109 | -2.400 | 0.021 | -27.007 | -2.315 |
| education | 0.3453 | 0.114 | 3.040 | 0.004 | 0.116 | 0.575 |
| income | 0.5975 | 0.089 | 6.687 | 0.000 | 0.417 | 0.778 |
| Omnibus: | 10.720 | Durbin-Watson: | 1.497 |
|---|---|---|---|
| Prob(Omnibus): | 0.005 | Jarque-Bera (JB): | 10.285 |
| Skew: | 1.013 | Prob(JB): | 0.00584 |
| Kurtosis: | 4.176 | Cond. No. | 462. |
Комментарии