import matplotlib.pyplot as plt

%matplotlib inline
%config InlineBackend.figure_format = 'svg'

Существуют три вида лжи: ложь, наглая ложь и статистика.

— Затасканный афоризм

Если в споре не хватает аргументов, ссылайтесь на статистику — и 9 из 10 поверят.

— Народная мудрость

Как использовать данные для обмана

Обман №1: Ошибки выборки

Составление выборки — это очень важно. Выборка должна быть репрезентативна относительно генеральной совокупности. Ошибка выборки — отклонение средних характеристик выборочной совокупности от средних характеристик генеральной совокупности.

Ошибки выборки бывают систематичекие и случайные.

Случайные ошибки выборки

Случайная ошибка — это вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала. К случайным ошибкам относят статистические погрешности, присущие самому выборочному методу. Они уменьшаются при возрастании объема выборочной совокупности. Случайную ошибку можно измерить методами математической статистики, если при формировании выборочной совокупности соблюдался принцип случайности, обеспечивающийся строго определенными правилами, которые составляют метод формирования выборочной совокупности, и устранить.

Систематические ошибки выборки

Систематические ошибки — результат деятельности самого исследователя. Они наиболее опасны, поскольку приводят к довольно значительным смещениям результатов исследования. Систематические ошибки считаются страшнее случайных еще и потому, что а) их невозможно оценить; б) они не уменьшается с увеличением выборки.

В результате систематической ошибки выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Особенность ошибки смещения состоит в том, что, являясь постоянной частью ошибки репрезентативности, она увеличивается с увеличением объема выборки.

Факторы:

нарушены методические и методологические правила проведения социологического исследования;
выбраны неадекватные способы формирования выборочной совокупности, методы сбора и расчета данных;
произошла замена требуемых единиц наблюдения другими, более доступными;
отмечен неполный охват выборочной совокупности (недополучение анкет, неполное их заполнение, труднодоступность единиц наблюдения).

Самый известный случай предвзятой выборки — опрос Literary Digest в 1936 году. По его результатам на выборах президента США должен был победить Альфред Лэндон. Показательно то, что для исследования проводимого Литерари Дайджест было отобрано более 2 млн. респондентов. На самих же выборах победил Теодор Рузвельт, победу которого предсказывали Гэлап и Роупер на основе опроса всего 4000 человек.

В чём была ошибка Literary Digest?

Другой пример предвзятой выборки — армейская лотерея в США в конце 60-х годов. В США в 1969 году каждому из дней года в случайном порядке с помощью лототрона были присвоены номера от 1 до 366. Призыву в первую очередь подлежали молодые люди 1945-1950 годов рождения, родившиеся в дни, которым выпали наименьшие номера. Почему-то, вышло так, что раньше всех отправлялись служить родившиеся в ноябре-декабре.

Почему?

Ещё один пример предвзятой выборки — опрос выпускников университетов об их зарплатах. Почему эти данные оказывались завышенными?

Обман №2: Выбираем среднее «правильно»

— Какова средняя температура больных в энской больнице?

— 36,6 °С, включая морг!

Чиновники едят мясо, я — капусту. В среднем мы едим голубцы.

Меры средний тенденций

Арифметическое среднее
Среднее геометрическое
Среднее гармоническое
Винсоризованное среднее
Усечённое среднее
Медиана
Мода и др.

Обман №3: умалчиваем о нюансах

Нюанс №1 — слишком маленькая, а значит, статистически некорректная выборка, повторяемая много раз.

Пример — испытать зубную пасту на десятке человек и зафиксировать улучшение, если оно есть, умолчать, если его нет. В какой-то момент удача улыбнётся.

Пример: испытание противополиомиелитной вакцины. В некой местности были вакцинированы 450 детей, а 680 детей остались непривитыми (в качестве контрольной группы). Вскоре после этого в той местности случилась эпидемия полиомиелита. Ни у одного из вакцинированных детей не было выявлено полиомиелита, как не было его выявлено и у детей из контрольной группы. Что проглядели экспериментаторы (или просто не поняли), когда планировали свое испытание, так это редкость паралитического полиомиелита. В обычном случае в группе такой численности можно ожидать всего двух случаев заражения, так что испытание с самого начала было совершенно бессмысленным. Потребовалась бы группа численностью раз в пятнадцать, а то и в двадцать пять больше, чтобы получить сколько-нибудь значимый результат.

Нюанс №2, который часто предпочитают не указывать — размах исследуемого признака или диапазон отклонения от указанного среднего. Не доверяйте особо среднестатистическим показателям, графикам и тенденциям, когда вам предъявляют их без тех важных цифр, что могли бы прояснить смысл.

Пример: многое в американском жилом строительстве планировалось таким образом, чтобы соответствовать размеру среднестатистической семьи из 3,6 человека. В переводе на язык реальности это означает семью из трех или четырех человек, что, в свою очередь, предполагает необходимость в доме двух спален. А семья такого размера, какой бы «среднестатистической» она ни считалась, в Америке находится в меньшинстве.

Пример: в книге «Нормы развития Гезелла» говорится, что ввозрасте стольких-то месяцев ребенку уже полагается сидеть. А поскольку примерно половина детей к указанному возрасту все еще не научилась сидеть, делает несчастными многих имногих родителей. Разумеется, говоря языком математики, их страдания уравновешиваются радостью другой половины родителей, обнаруживших, что у них вполне «развитые» дети. Зато большой вред могут причинить старания несчастных родителей подстегнуть развитие своего ребенка, чтобы он соответствовал норме и больше не считался недоразвитым.

Обман №4: много шума практически из ничего

Допустим, мы, выяснили, что у Питера коэффициент умственного развития (IQ) составил 98, а у Линды – 101, при этом в тесте на IQ коэффициент 100 принят за средний, то есть нормальный уровень. Значит ли это, что Линда у нас одареннее Питера, ее умственное развитие выше среднего, ау Питера – ниже среднего?

Конечно нет. Почему?

Обман №5: строим выгодные для себя графики

A Quick Guide to Spotting Graphics That Lie

Начало координат не в 0

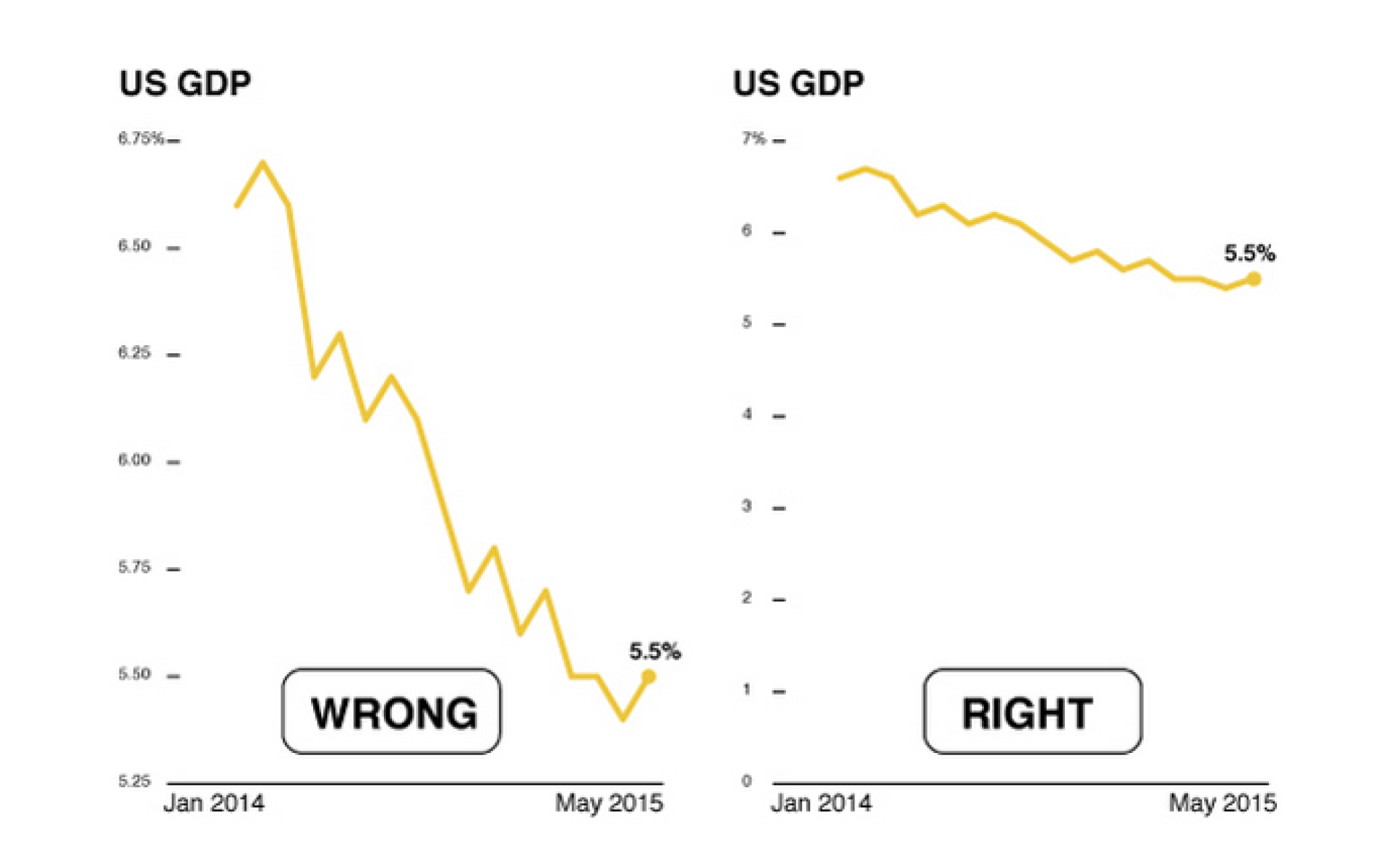
Разные шкалы на одном графике

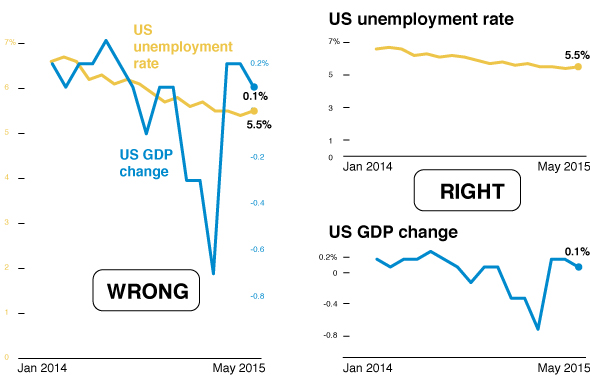
Корреляция ≠ причинность

http://www.tylervigen.com/spurious-correlations

Не нормируем на размер популяции

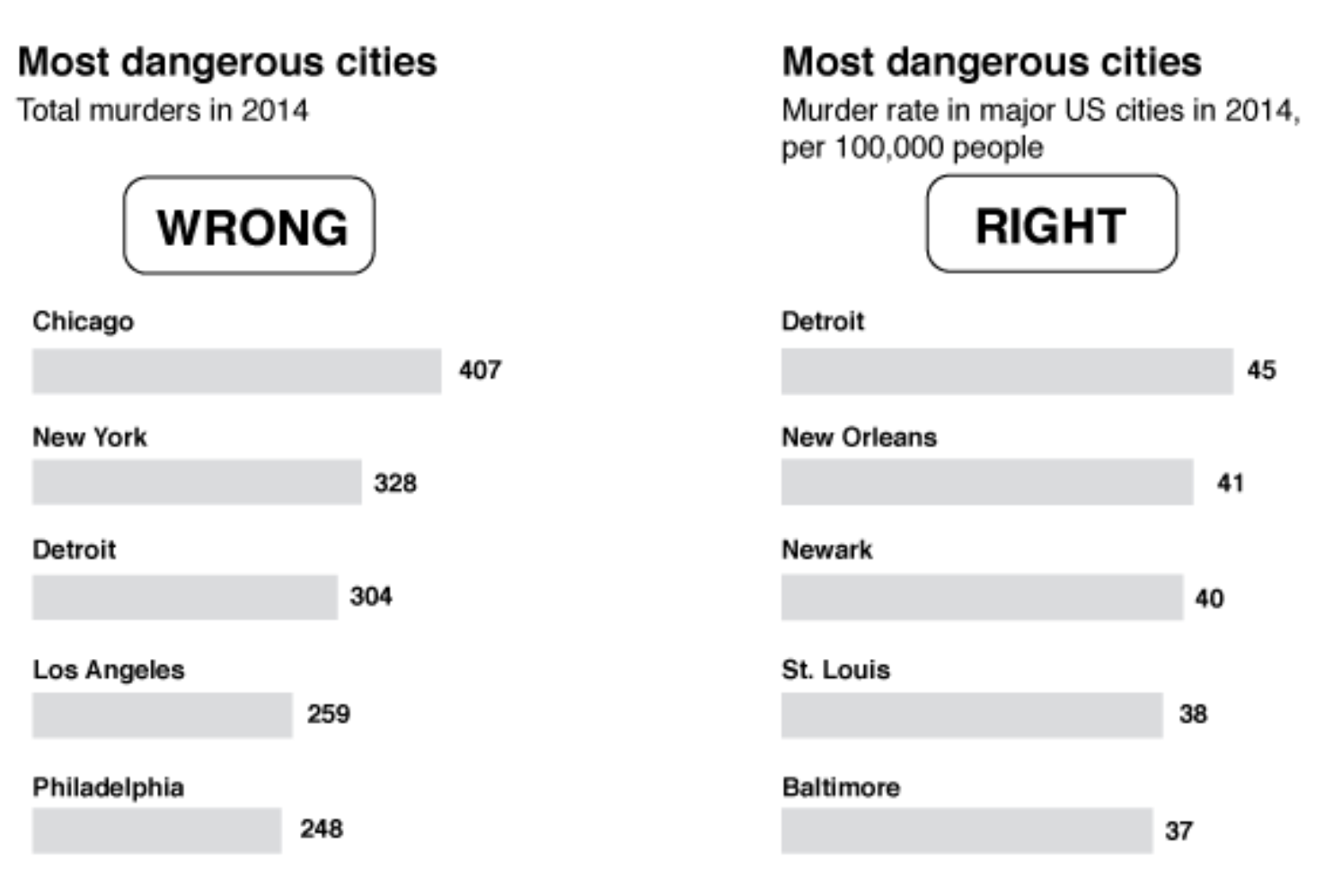
Излишне увлекаемся перспективой

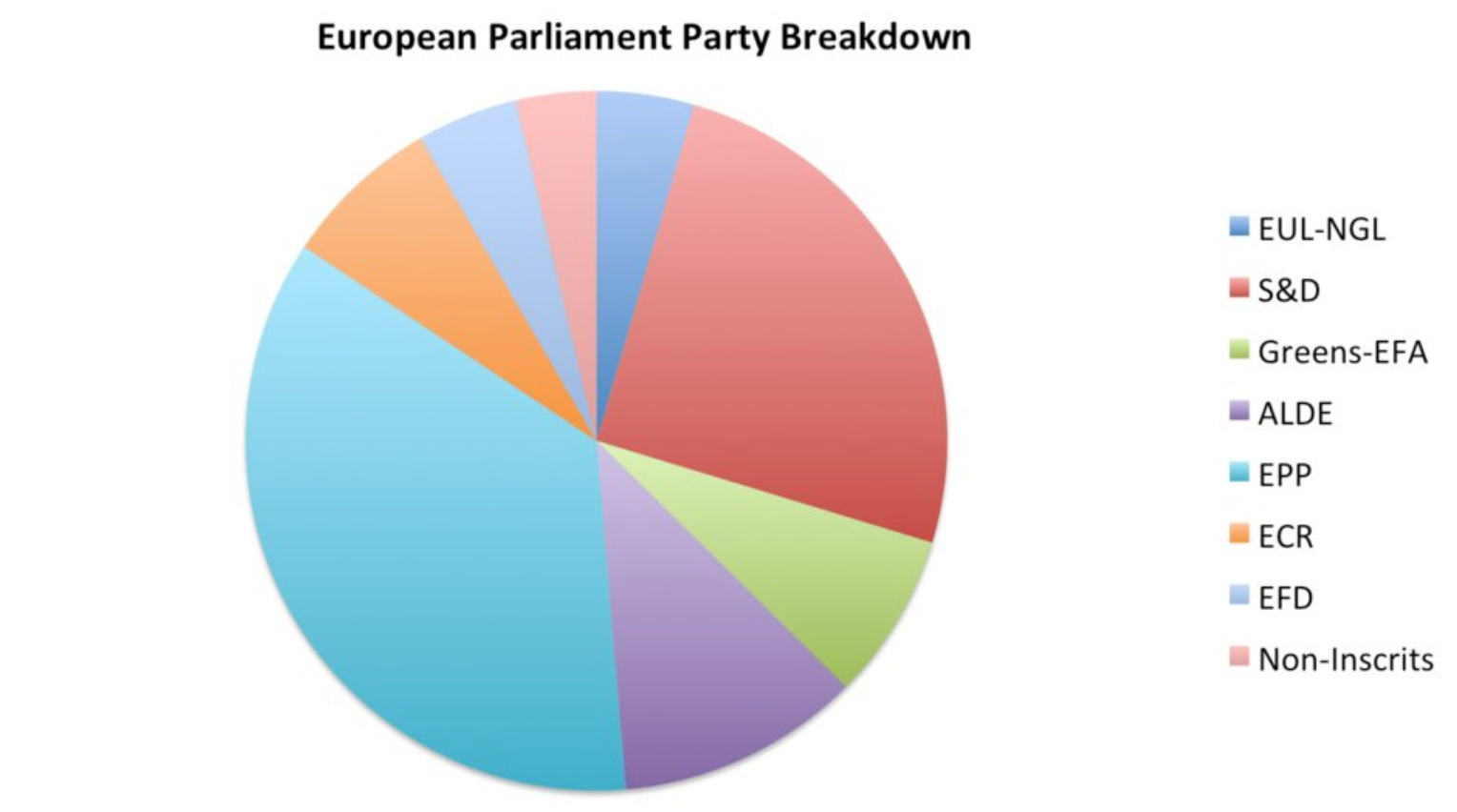
В инфографике забываем, что площадь фигуры = произведению её сторон

False Visualizations: Sizing Circles in Infographics

Увлекаемся экстраполяцией

Обман № 6: Используем псевдообоснованные данные

Любую количественную величину несложно выразить множеством разнообразных способов. Вы можете, например, представить один и тот же факт, называя его доходностью продаж в 1%, рентабельностью инвестиций в 15%, десятимиллионной прибылью, ростом прибылей на 40% (по сравнению со средним показателем за 1935–1939 гг.) или сокращением на 60% по сравнению с предыдущим годом. Суть в том, чтобы выбрать формулировку, которая лучше всего подходит для текущих надобностей. А после остается уповать на то, что лишь единицы, читая эту информацию, сообразят, насколько она искажает реальное положение дел.

Уровень смертности в военно-морском флоте США в период Испано-Американской войны 1898 г. составлял девять человек на тысячу. За тот же период уровень смертности среди гражданского населения Нью-Йорка достигал шестнадцати человек на тысячу. Позже эти цифры использовали вербовщики, чтобы показать: служить в ВМС безопаснее, чем находиться за его пределами.

Допустим, что сами эти цифры точны. Что тут не так?

До и после занятия спортом. Что тут не так?

Данные против интуиции

Феномен Уилла Роджерса

Парадокс Симпсона

Парадокс инспекции

Почему при ожидании автобуса, который приходит в среднем каждые 10 минут, ваше среднее время ожидания будет около 10 минут (во всяком случае, точно больше 5)?

Парадокс дружбы

Парадокс Берксона

Внеклассное чтение

Проблемы интерпретации моделей

Метрики качества

При помощи метрик качества мы можем оценивать, насколько хорошо наши модели справляются с поставленной задачей. Метрики качества могут совпадать с функцией потерь, а могут и нет.

Функция потерь — функция, которая в теории статистических решений характеризует потери при неправильном принятии решений на основе наблюдаемых данных. Если решается задача оценки параметра сигнала на фоне помех, то функция потерь является мерой расхождения между истинным значением оцениваемого параметра и оценкой параметра.

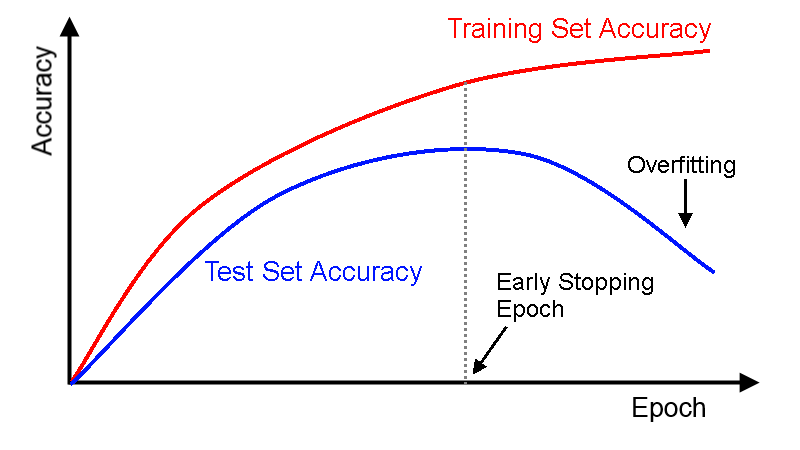
Early stopping

Accuracy не можнт выступать в качестве фукнции потерь, но может использоваться как метрика оценки качества. Показания метрики качества и функции потерь могут значительно расходиться. Для максимизации метрики качества придумана техника ранней остановки.

Метрики качества для регрессионных моделей

Итак, у нас имеет модель $\hat{y}= f(x)=w_0+\sum_{i=1}^n w_i x_i$

Среднеквадратическая ошибка (MSE).

Для вычисления среднеквадратической ошибки все отдельные остатки регрессии возводятся в квадрат, суммируются, сумма делится на общее число ошибок:

$\frac 1N\sum_{i=1}^N(y_i-\hat{y}_i)^2$

y_true = np.array([4, 6, 9, 30])

def mse(y_true, y_pred):
    step1 = ((y_true - y_pred) ** 2)

    if isinstance(step1, (int, float)):
        return step1
    else:
        return sum(step1) / len(y_true)

print(mse(y_true, y_true-1), mse(y_true, y_true-5))

1.0 25.0

plt.figure(figsize=(10, 5))

for n in y_true.tolist():
    x = []
    y = []
    for i in np.arange(-5, 5, .1).tolist():
        x.append(n+i)
        y.append(mse(n, n + i))
    plt.plot(x, y, label=f"true y = {n}")

plt.legend()
plt.title(label="Графики ошибок для каждого значения")
plt.ylabel("MSE")
plt.xlabel("y true")

Text(0.5, 0, 'y true')

Преимущества функции:

дифференцируемость

Продифференцируйте функцию и найдите константу, которая обеспечит наилучшие предсказания.

plt.figure(figsize=(10, 5))

for n in y_true.tolist():
    x = []
    y = []
    for i in np.arange(-15, 15, .1).tolist():
        x.append(n+i)
        y.append(mse(n, n + i))
    plt.plot(x, y, label=f"true y = {n}")



x_const = []
y_const = []
for i in np.arange(-3, 35, .1).tolist():
    x_const.append(i)
    y_const.append(mse(i, y_true.mean()))
plt.plot(x_const, y_const, label=f"График производной при константном значении")

plt.legend()
plt.title(label="Графики ошибок для каждого значения")
plt.ylabel("MSE")
plt.xlabel("y true")

Text(0.5, 0, 'y true')

Особенности:

использование квадратичной функции делает особый акцент на объектах с сильной ошибкой, поэтому метод обучения будет в первую очередь стараться уменьшить отклонения на таких объектах. Если же эти объекты являются выбросами (то есть значение целевой переменной на них либо ошибочно, либо относится к другому распределению и должно быть проигнорировано), то такая расстановка акцентов приведёт к плохому качеству модели.

Недостатки:

функция не очень хорошо интерпретируется, поскольку не сохраняет единицы измерения. Если мы предсказываем цену в рублях, то MSE будет измеряться в квадратах рублей. Чтобы избежать этого, используют корень из среднеквадратичной ошибки.
Самое по себе значение MSE мало о чем говорит т.к. оно не нормированно.

Корень из среднеквадратической ошибки (RMSE)

$RMSE = \sqrt{\frac 1N\sum_{i=1}^N(y_i-\hat{y}_i)^2} = \sqrt{MSE}$

$\frac{\partial RMSE}{\partial \hat{y_i}} = \frac{1}{2\sqrt{MSE}}\frac{\partial MSE}{\partial \hat{y_i}}$

Производная от RMSE представляет собой то же самое, что производная по MSE, только с коэффициентом, зависящим от самой MSE.

Коэффициент детерминации $R^2$

Коэффициент детерминации измеряет долю дисперсии, объяснённую моделью, в общей дисперсии целевой переменной. $R^2=1 - \frac{\sum_{i=1}^n(y_i-\hat{y}<em>i)^2}{\sum</em>{i=1}^n(y_i-\bar y)^2}$ Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.

Другими словами $R^2=\frac{SSR}{SST}=\frac{сумма \ квадратов \ регрессии}{полная \ сумма \ квадратов}=\frac{изменчивость, \ объяснимая \ линейной \ зависимостью}{изменчивость, \ объяснимая \ линейной \ зависимостью \ и \ ошибкой}$

Средняя абсолютная ошибка (MAE)

$\frac 1N\sum_{i=1}^N|y_i-\hat{y}_i|$ Модуль отклонения не является дифференцируемым, но при этом менее чувствителен к выбросам, чем квадрат отклонения MSE.

Наилучший константный предиктор для MSE — медиана.

def mae(y_true, y_pred):
    step1 = abs(y_true - y_pred)

    if isinstance(step1, (int, float)):
        return step1
    else:
        return sum(step1) / len(y_true)

plt.figure(figsize=(10, 5))

for n in y_true.tolist():
    x = []
    y = []
    for i in np.arange(-5, 5, .1).tolist():
        x.append(n+i)
        y.append(mae(n, n + i))
    plt.plot(x, y, label=f"true y = {n}")

x_const = []
y_const = []
for i in np.arange(0, 35, .1).tolist():
    x_const.append(i)
    y_const.append(mae(i, np.median(y_true)))
plt.plot(x_const, y_const, label=f"График производной при константном значении")

plt.legend()
plt.title(label="Графики ошибок для каждого значения")
plt.ylabel("MAE")
plt.xlabel("y true")

Text(0.5, 0, 'y true')

В чем разница с MSE и для каких случаев MAS подходит лучше?

Средняя квадратичная процентная ошибка (mean square percentage error, MSPE) и средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE)**

$\frac 1N\sum_{i=1}^N \Big( \frac{y_i-\hat{y}<em>i}{y_i} \Big)^2$ $\frac 1N\sum</em>{i=1}^N \Bigl\lvert \frac{y_i-\hat{y}_i}{y_i} \Bigr\rvert$

def mspe(y_true, y_pred):
    step1 = ((y_true - y_pred) ** 2) / y_true

    if isinstance(step1, (int, float)):
        return step1
    else:
        return sum(step1) / len(y_true)

def mape(y_true, y_pred):
    step1 = abs(y_true - y_pred) / y_true

    if isinstance(step1, (int, float)):
        return step1
    else:
        return sum(step1) / len(y_true)

fig, axes = plt.subplots(nrows=1, ncols=2)
fig.set_size_inches(12, 5)

kinds = [mspe, mape]
for kind_num, kind in enumerate(kinds):
    for n in y_true.tolist():
        x = []
        y = []
        for i in np.arange(-5, 5, .1).tolist():
            x.append(n+i)
            y.append(kind(n, n + i))
        axes[kind_num].plot(x, y, label=f"true y = {n}")
        axes[kind_num].set_title(f'График для {kind.__name__.upper()}')
        axes[kind_num].set_ylabel(f'{kind.__name__.upper()}')

Объясните, что мы видим на этих графиках.

Чем больше абсолютное значение наблюдения, тем меньше мы его штрафуем за единицу ошибки.

Среднеквадратичная логарифмическая ошибка (mean squared logarithmic error, MSLE)

$MSLE=\frac{1}{N}\sum_{i=1}^N(\log(y_i+1)-\log(\hat{y}_i+1))^2$

За счёт логарифмирования ответов и прогнозов мы скорее штрафуем за отклонения в порядке величин, чем за отклонения в их значениях. Также следует помнить, что логарифм не является симметричной функцией, и поэтому данная функция потерь штрафует заниженные прогнозы сильнее, чем завышенные.

def msle(y_true, y_pred):
    step1 = (np.log(y_true + 1) - np.log(y_pred + 1)) ** 2

    if isinstance(step1, (int, float)):
        return step1
    else:
        return sum(step1) / len(y_true)

fig, axe = plt.subplots()
fig.set_size_inches(12, 5)


for n in y_true.tolist():
    x = []
    y = []
    for i in np.arange(-3, 6, .1).tolist():
        x.append(n+i)
        y.append(msle(n, n + i))
    axe.plot(x, y, label=f"true y = {n}")
    axe.set_title('График для MSLE')
    axe.set_ylabel('MSLE')

В каких случаях лучше использовать MSLE?

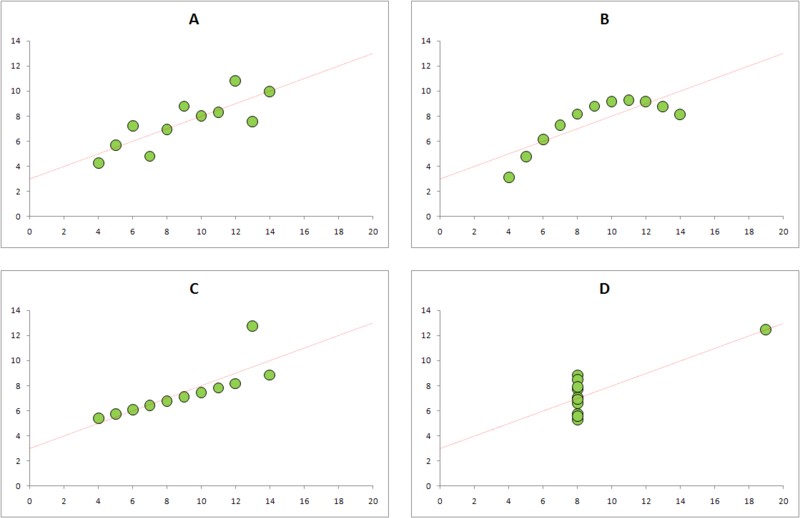
⚠️Осторожно! Не всегда можно полагаться на цифры. Если это возможно, лучше также построить график зависимости $y$ от $x$ . Это позволит Вам избежать попадания в ловушку квадрата Энскомба. Основные числовые характеристики этих данных идентичны и все эти зависимости описываются формулой $y = 3 + 0.5x$ , но, очевидно, выглядят они по-разному:

Метрики качества классификаторов

В sklearn
What’s WRONG with Metrics?
Лекции Владимира Соколова

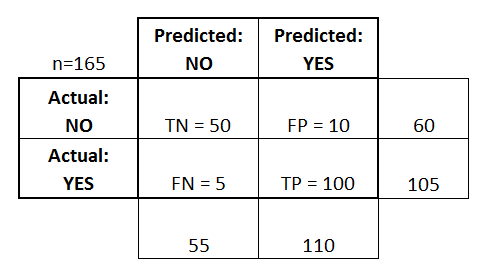
Матрица ошибок (Confusion matrix)

Матрица ошибок — это способ разбить объекты на четыре категории в зависимости от комбинации истинного ответа и ответа алгоритма.

Основные термины:

$TP$ — истино-положительное решение;
$TN$ — истино-отрицательное решение;
$FP$ — ложно-положительное решение (Ошибка первого рода);
$FN$ — ложно-отрицательное решение (Ошибка второго рода).

Интерактивная картинка с большим числом метрик

Accuracy

Наиболее очевидной мерой качества в задаче классификации является доля правильных ответов (accuracy). Например, если мы классифицируем картинки кошек, accuracy показывает долю правильных ответов.

$\mathrm {Accuracy} ={\frac {\mathrm {TP} +\mathrm {TN} }{P+N}}={\frac {\mathrm {TP} +\mathrm {TN} }{\mathrm {TP} +\mathrm {TN} +\mathrm {FP} +\mathrm {FN} }}$

Первая проблема аккуратности в том, что её они недифференцируема.

В чём вторая проблема?

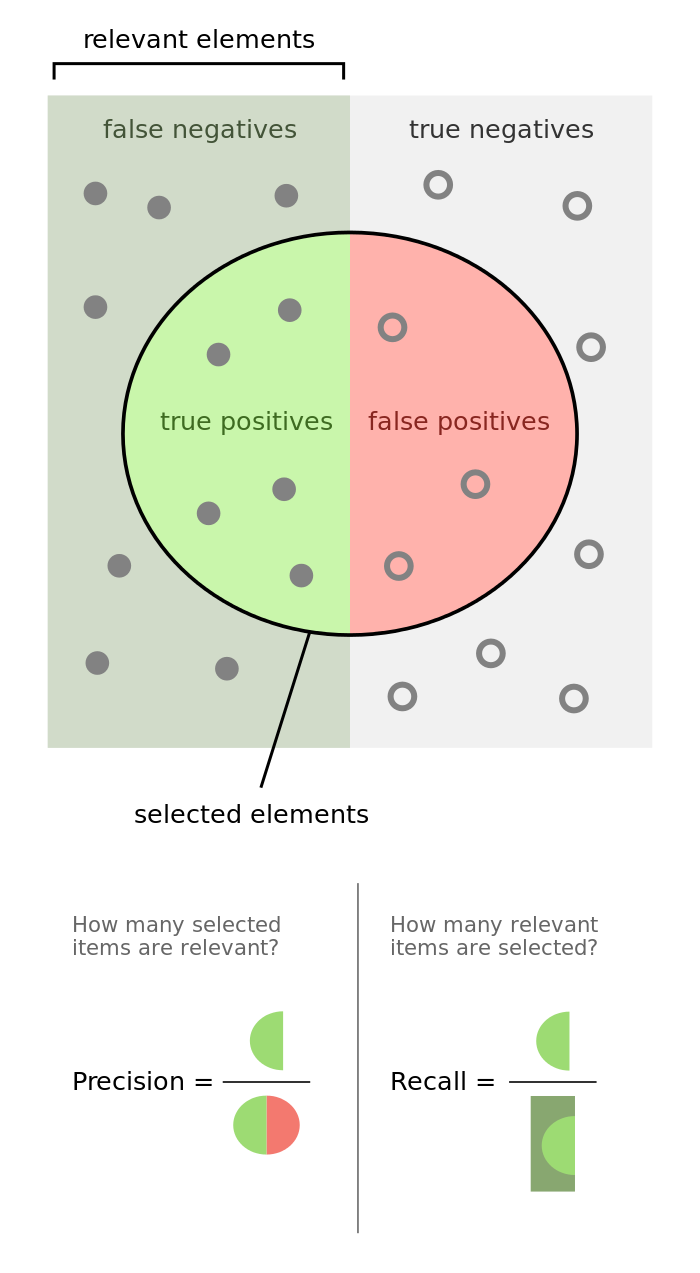
Точность (precision) и полнота (recall)

Более информативными критериями являются точность (precision) и полнота (recall). Они не зависят от соотношения размеров классов.

Точность показывает, какая доля объектов, выделенных классификатором как положительные, действительно является положительными: $Precision = \frac{TP}{TP+FP}$

Полнота показывает, какая часть положительных объектов была выделена классификатором: $Recall = \frac{TP}{TP+FN}$

Какую метрику следует максимизировать в задаче классификации раковых клеток? Что будет, если выбрать другую метрику из этих двух?

F-мера, гармоническое среднее точности и полноты

F_\beta = (1 + \beta^2) \cdot \frac{\mathrm{precision} \cdot \mathrm{recall}}{(\beta^2 \cdot \mathrm{precision}) + \mathrm{recall}} = \frac {(1 + \beta^2) \cdot \mathrm{true\ positive} }{(1 + \beta^2) \cdot \mathrm{true\ positive} + \beta^2 \cdot \mathrm{false\ negative} + \mathrm{false\ positive}}

Среднее гармоническое обладает важным свойством — оно близко к нулю, если хотя бы один из аргументов близок к нулю. Именно поэтому оно является более предпочтительным, чем среднее арифметическое (если алгоритм будет относить все объекты к положительному классу, то он будет иметь recall = 1 и precision больше 0, а их среднее арифметическое будет больше 1/2, что недопустимо).

Чаще всего берут $\beta=1$ , хотя иногда встречаются и другие модификации. $F_2$ острее реагирует на recall (т. е. на долю ложноположительных ответов), а $F_{0.5}$ чувствительнее к точности (ослабляет влияние ложноположительных ответов).

В sklearn есть удобная функция sklearn.metrics.classification_report, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.

AUC-ROC

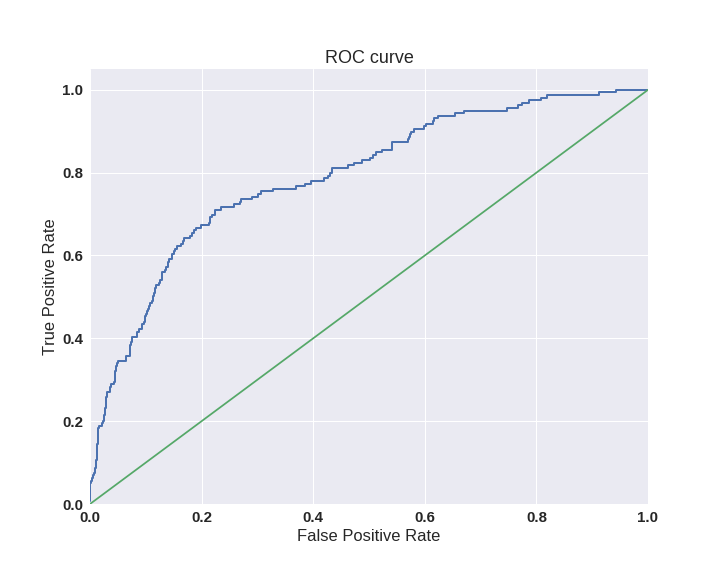
Кривая ошибок или ROC-кривая – графичекая характеристика качества бинарного классификатора, зависимость доли верных положительных классификаций от доли ложных положительных классификаций при варьировании порога решающего правила.

Данная кривая представляет из себя линию от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR):

$\large TPR = \frac{TP}{TP + FN}$

$\large FPR = \frac{FP}{FP + TN}$

True positive rate (TPR, sensitivity, recall, probability of detection) — показывает, какую долю из объектов positive класса алгоритм предсказал верно.

False positive rate (FPR) показывает, какую долю из объектов negative класса алгоритм предсказал неверно.

True negative rate (TNR, specificity) — показывает, какую долю из объектов negative класса алгоритм предсказал верно.

Критерий AUC-ROC более устойчив к несбалансированным классам и может быть интерпретирован как вероятность того, что случайно выбранный positive объект будет проранжирован классификатором выше (будет иметь более высокую вероятность быть positive), чем случайно выбранный negative объект.

Однако, баланс классов все равно важен. Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеет-ся 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм, идеально решающий задачу, то его TPR будет равен еди- нице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма. Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных.

В таким случаях можно использовать AUC-PR — площадь под кривой, простроенной в системе координат $y=precision$ и $x=recall$ pdf.

Индекс Джини.

В задачах кредитного скоринга вместо AUC-ROC часто используется пропорциональная метрика, называемая индексом Джини (Gini index): $\large Gini = 2AUC − 1.$

По сути это площадь между ROC-кривой и диагональю соединяющей точки (0,0) и (1, 1).

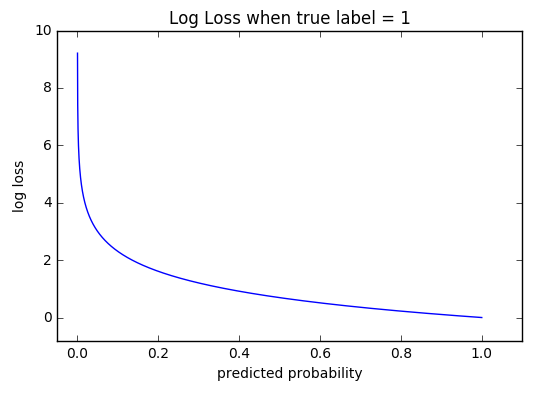
LogLoss

Для бинарной классификации:

$-\frac1N \sum_{i=1}^{N}(y_i\log(\hat{y_i}) + (1 - y_i)\log(1 - \hat{y_i}))$

Для мультиклассовой классификации: $-\frac1N \sum_{i=1}^{N} \sum_{l=1}^{L} y_{il}\log(\hat{y_{il}})$

Работает с вероятностными предсказаниями.

Улетает в бесконечность при очень больших ошибках.

Каппа Кохена

$1 - \frac{1 - accuracy}{1 - p_e} = 1 - \frac{error}{baseline \ error},$

где $p_e$ — средняя аккуратность на подвыборках предсказаний.

Landis, J.R.; Koch, G.G. (1977). “The measurement of observer agreement for categorical data”. Biometrics 33 (1): 159–174
Видео с объяснением

Каппа Кохена может также быть взвешенной, т.е. штрафовать за ошибку разных классов по-разному. Формула от этого почти не меняется. Просто считаем взвешенные ошибки, вместо обычных. Эту модификацию удобно применять для классификации упорядоченных классов.

Вопрос 1

Предположим, что мы решаем задачу бинарной классификации, метрика качества — логлосс. Какие прогнозы более предпочтительны для этой метрики качества, если истинными метками являются [0, 0, 0, 0].

[0, 0, 0, 1]
[0.4, 0.5, 0.5, 0.6]
[0.5, 0.5, 0.5, 0.5]

Вопрос 2

Предположим, что целевая метрика R-квадрат. Какие функции потерь нам следует использовать для наших моделей?

RMSLE
MAE
RMSE
AUC
MSE

Вопрос 3

Подсчитайте AUC для таких предсказаний:

true	predicted
1	0.83
0	0.44
1	0.69
0	0.12
0	0.03
1	0.21

Выбор параметров модели

Главная задача обучаемых алгоритмов – их способность обобщаться, то есть хорошо работать на новых данных. Для того, чтобы алгоритм при обучении при обучении приобрёл наибольшую обобщающую способность нам необходимо подобрать значения гиперпараметров.

Вопрос с реального собеседования: что такое гиперпараметры? Привидите примеры.

Но тут над подстерегает опасность, под названием bias-variance tradeoff.

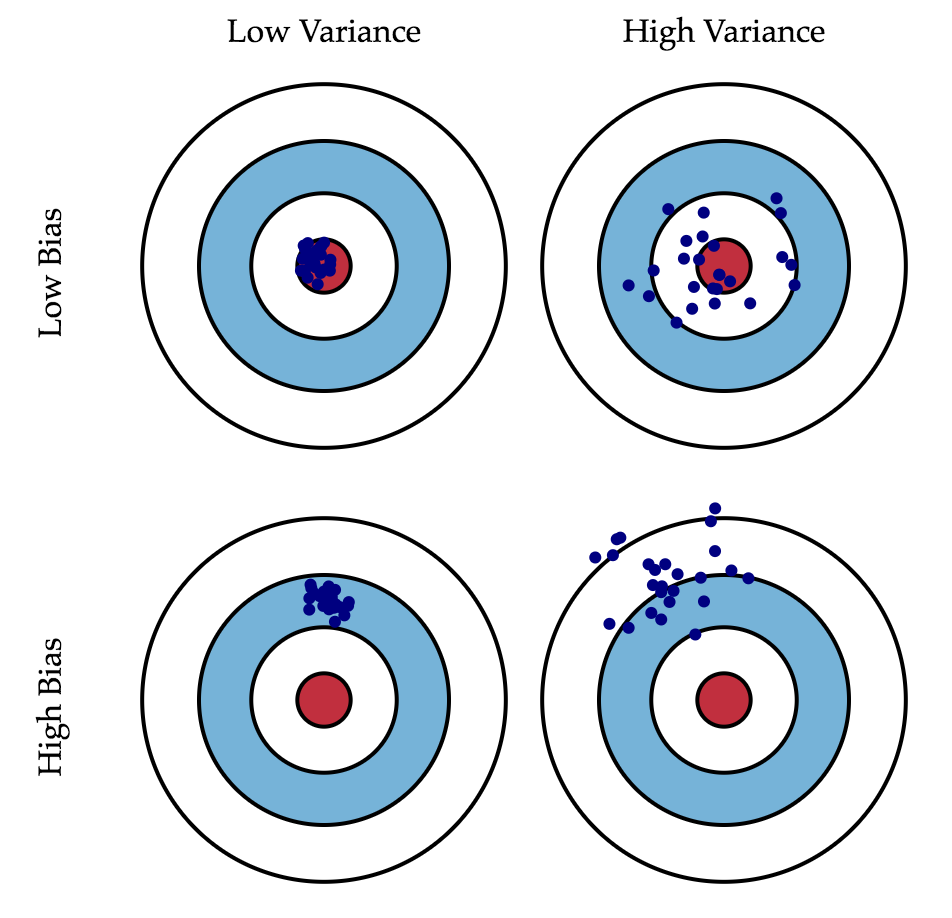Смещение - это ошибка от ошибочных предположений в алгоритме обучения. Высокое смещение может привести к тому, что алгоритм упустит соответствующие отношения между функциями и целевыми выходами (underfitting).

Дисперсия - это ошибка от чувствительности к небольшим колебаниям в тренировочном наборе. Высокая дисперсия может привести к тому, что алгоритм моделирует случайный шум в данных обучения, а не предполагаемые выходы (overfitting).

Для борьбы с переобучением существуют множество методов:

Собрать больше данных
Кросс-валидация
Регуляризация
- Удаление или снижение веса признаков
- Drop-out
- Ранняя остановка
Ансамбли алгоритмов
и др.

Кросс-валидация

Поскольку на новых данных мы сразу не можем проверить качество построенной модели (нам ведь надо для них сделать прогноз, то есть истинных значений целевого признака мы для них не знаем), то надо пожертвовать небольшой порцией данных, чтоб на ней проверить качество модели.

Проблема 1: Приходится слишком много объектов оставлять в контрольной подвыборке. Уменьшение длины обучающей подвыборки приводит к смещённой (пессимистически завышенной) оценке вероятности ошибки.
Проблема 2: Оценка существенно зависит от разбиения, тогда как желательно, чтобы она характеризовала только алгоритм обучения.
Проблема 3: Оценка имеет высокую дисперсию, которая может быть уменьшена путём усреднения по разбиениям.

Но это ещё не кросс валидация. При кросс-валидации имеющиеся в наличии данные разбиваются на k частей. Затем на k−1 частях данных производится обучение модели, а оставшаяся часть данных используется для тестирования. Процедура повторяется k раз; в итоге каждая из k частей данных используется для тестирования. В результате получается оценка эффективности выбранной модели с наиболее равномерным использованием имеющихся данных.

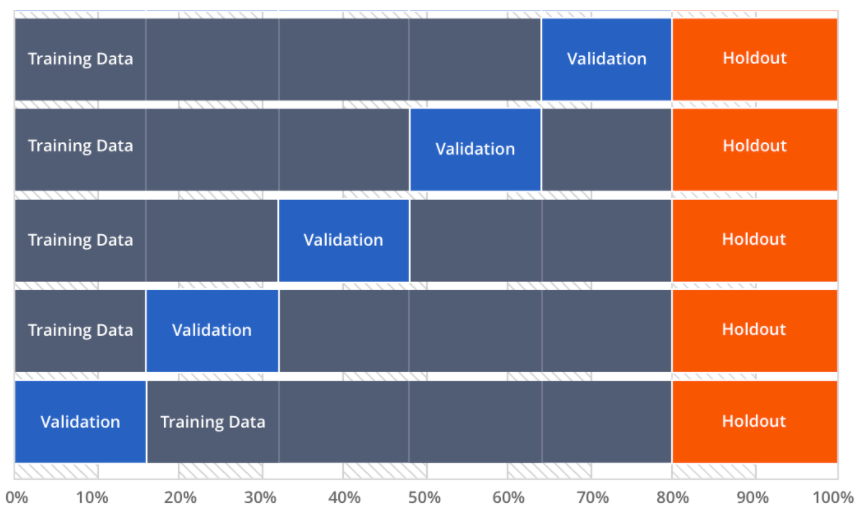
k можно выбирать от 2 до n (размера обучающей выборки).

Если k = n, подход называется leave-one-out CV (LOOCV), когда оценка ошибки происходит на одном наблюдении.

Чем меньше k, тем меньше дисперсия ошибки
Чем больше k, тем меньше смещение ошибки
Чем больше k, тем больше моделей обучаем (дорого)

Из курса How to Win a Data Science Competition: Learn from Top Kagglers

Подбор гиперпараметров модели по сетке

Суть подбора по сетке в том, что мы строим модель разными комбинациями параметров, после чего оцениваем качество модели на валидационных данных.

Самое важное здесь — знать, какие параметры и в каких моделях подбирать.

Из курса How to Win a Data Science Competition: Learn from Top Kagglers

Ансамблирование алгоритмов

Cтекинг (Stacking) и блендинг (Blending)

Этические вопросы в области искуственного интеллекта

Как использовать данные для обмана

Обман №1: Ошибки выборки

Случайные ошибки выборки

Систематические ошибки выборки

Обман №2: Выбираем среднее «правильно»

Обман №3: умалчиваем о нюансах

Обман №4: много шума практически из ничего

Обман №5: строим выгодные для себя графики

Начало координат не в 0

Разные шкалы на одном графике

Корреляция ≠ причинность

Не нормируем на размер популяции

Излишне увлекаемся перспективой

В инфографике забываем, что площадь фигуры = произведению её сторон

Увлекаемся экстраполяцией

Обман № 6: Используем псевдообоснованные данные

Данные против интуиции

Феномен Уилла Роджерса

Парадокс Симпсона

Парадокс инспекции

Парадокс дружбы

Парадокс Берксона

Внеклассное чтение

Проблемы интерпретации моделей

Метрики качества

Early stopping

Метрики качества для регрессионных моделей

Среднеквадратическая ошибка (MSE).

Корень из среднеквадратической ошибки (RMSE)

Коэффициент детерминации R2R^2R2

Средняя абсолютная ошибка (MAE)

Средняя квадратичная процентная ошибка (mean square percentage error, MSPE) и средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE)**

Среднеквадратичная логарифмическая ошибка (mean squared logarithmic error, MSLE)

Метрики качества классификаторов

Матрица ошибок (Confusion matrix)

Accuracy

Точность (precision) и полнота (recall)

F-мера, гармоническое среднее точности и полноты

AUC-ROC

Индекс Джини.

LogLoss

Каппа Кохена

Вопрос 1

Вопрос 2

Вопрос 3

Выбор параметров модели

Кросс-валидация

Подбор гиперпараметров модели по сетке

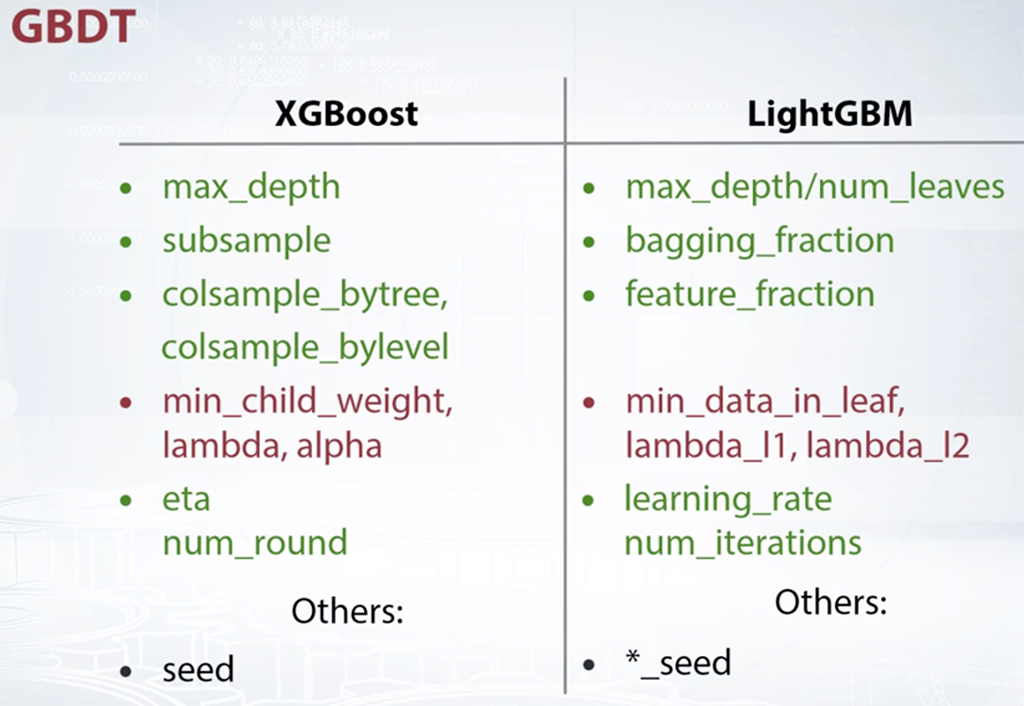
Ансамблирование алгоритмов

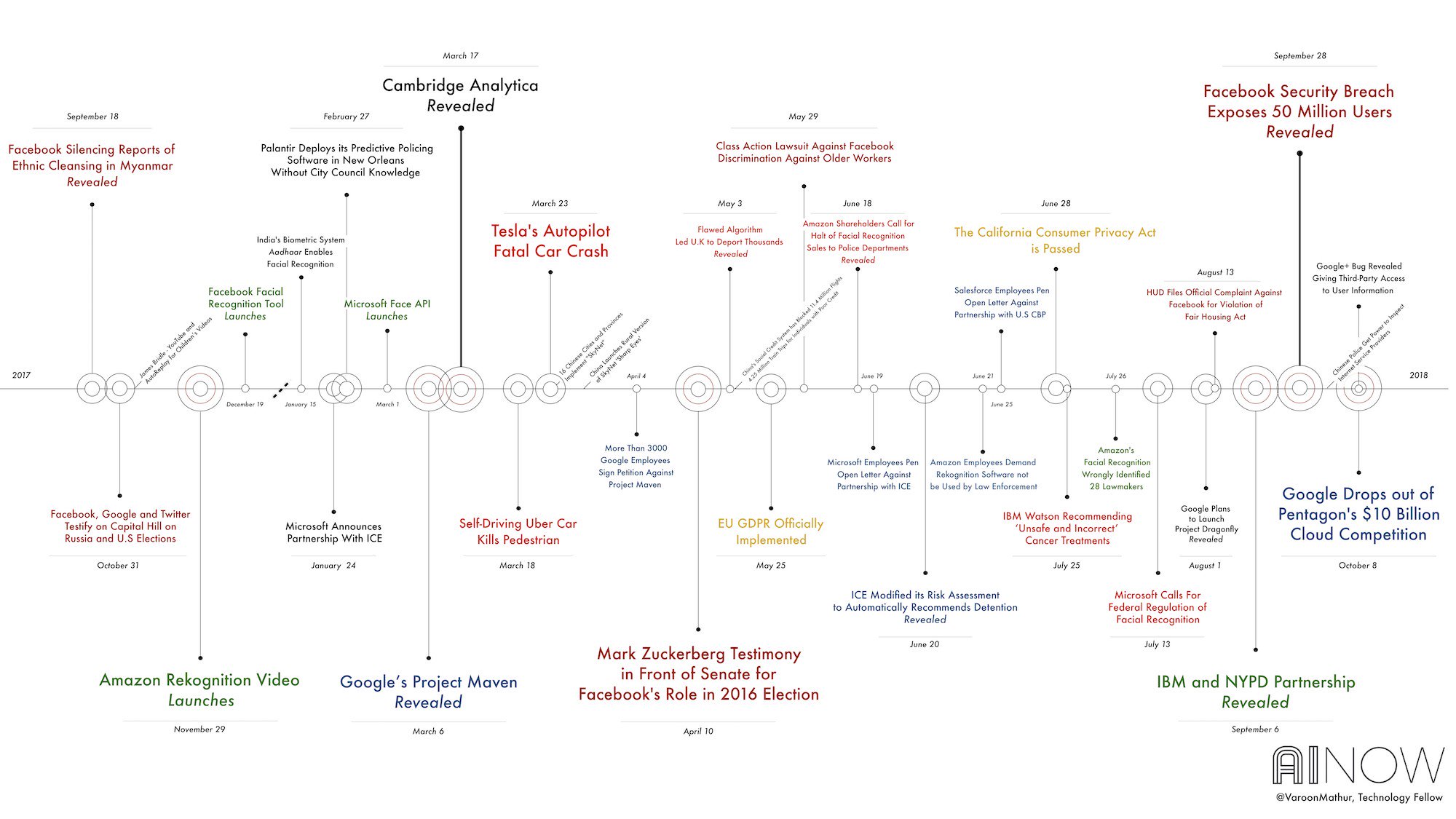
Этические вопросы в области искуственного интеллекта

Ссылки

Комментарии

Коэффициент детерминации $R^2$