Прогнозирование временных рядов
Введение
Все хотят уметь прогнозировать временные ряды, ведь это означало бы научиться предсказывать цены на акции курс валют, и, менее очевидный вариант, голосовые записи. Все хотят, однако немногие могут — проблема прогнозирования до сих пор не решена с более-менее приемлимым качеством, и, самое печальное, не факт, что это вообще возможно из-за так называемого парадокса предсказания [1]. Парадокс предсказания заключается в том, что даже если мы научимся предсказывать какие-либо социальные процессы, наши предсказания быстро станут неактуальны, поскольку сам их факт наличия будет влиять на действия людей. Если брать пример из социальных наук, то можно упомянуть предсказания Карла Маркса, который утверждал, что капитализм обречён на крах, поскольку развившись до стадии имперализма он выжимает из рабочих все соки, а поэтому у них непременно пробудится классовое самосознание и они поднимуться на борьбу.
Капиталисты сами продадут нам веревку, на которой мы их повесим В.И. Ленин
Капиталисты, услышав и восприняв это нерадостное для них пророчество, решили поступиться малым чтобы сохранить многое и придумали пенсии, социальносе государство, обязательное медицинское страхование и социально-ответственное предпринимательство (ха-ха). Всё это свело на нет классовую ненависть, поскольку на стороне капиталистов стал выступать средний класс, используемый в роли буфера между двумя полисами, да и границы самих классов почти размылись. Поэтому, хоть и состояние 26 богатейших миллиардеров совсем недавно сравнялось с доходами 3.8 миллиарда самых бедных людей мира [2], все довольны и не ропчат.
Кстати, раз уж мы стали приводить примеры из социальных наук, интересно, что парадокс предсказания в некоторой степени противоречит другому известному принципу, который называется теоремой Томаса или самоисполняющимся пророчеством. Он звучит следующим образом: «Если люди определяют ситуации как реальные, они реальны по своим последствиям». Термин «самоисполняющееся пророчество» ввёл в широкий оборот социолог Томас Мертон в своей одноимённой статье 1948 года [3]. В ней он описывает историю банка, в слухи о банкротстве которого поверило большое количество вкладчиков этого банка. Вкладчики решили забрать свои деньги, что в конечном счёте действительно привело к банкроству банка, а затем и к Чёрному вторнику — вестнику Великой депрессии. Этот пример наглядно показывает, как работает самоисполняющееся пропрочество — изначально ложное определение ситуации вызывает новое поведение, которое делает изначально ложное представление истинным.
Налицо аналогия с парадоксом предсказания, который также утверждает, что само наличие предсказания влияет на дальнейшние действия людей, только в случае с банком, предсказание не потеряло актуальность, а наоборот "подмяло" реальность под себя.
Теория временных рядов
Мы тут не за теорией, но некоторые основные понятия ввести тем не менее надо. За более глубоким разъяснением советую обратиться к учебникам Светуньковых (у них, кстати, есть сайт c блогом).
Итак, под временным рядом понимаются последовательно измеренные через некоторые (зачастую равные) промежутки времени данные. Например, люди на протяжении ста лет измерядли тепрературу воздуха в каком-то мести и получили временной ряд. Самое ценное, что можно делать с временными рядами — это прогнозировать их дальнейшние значения. Прогноз - это всегда вероятностное, но научно обоснованное суждение о созможных будущих состояниях объекта или явления, в нём всегда есть доля ошибки. В лучшем случае эта ошибка случайная, в худшем — систематическая (о видах ошибок читайте в лекции «честные модели»). Чтобы построить прогноз необходима математическая модель, которая задаст правило для его расчёта, причём эта модель будет стохастической, поскольку в ней обязательно присутствует неопределённость в виде ошибки.
Помимо этого на временных рядах можно тестировать различные гипотезы: есть ли между двумя временными рядами связь, являются ли они стационарными или нет. Стационарность — это свойство процесса не менять свои характеристики со временем, т.е. если во временном ряду есть какой-либо тренд, он уже не стационарен. Это неудобно, поскольку многие модели и тесты предполагают стационарность временных рядов, а на нестационарных рядах их результаты ненадёжны.
Модели прогнозирования
Классификация методов прогнозирования — это довольно спорная тема и какого-то канона здесь нет, поэтому можно особо не опасаться сделать ошибку. Но вначале я хотел бы выделить главную особенность задачи прогнозирования временных рядов по сравнению с другими задачами машинного обучения — предсказание целевой переменной обычно основывается ни на других признаках, а на значениях самой себя за предыдущий временной период. Таким образом, для прогнозирования временных рядов используются почти все те же модели, что и для любого другого прогнозирования, но с некоторыми, модификациями, предназначенными учесть эту их сосбенность.
В своей диссертации [4] Ирина Чучуева выделяет две основные группы моделей — статистические, где зависимость будущего значения от прошлого задается в виде некоторого уравнения (регрессионные модели, модель экспоненциального сглаживания), и структурыне, в которых эта зависимость задается в виде некоторой структуры и правил перехода по ней (нейронные сети, деревья решений). Основание этой системы классификации мне не совсем понятно. Получается, в этой классификации разделение идёт всего лишь по признаку, является ли модель линейной функцией или композицией линейных и нелинейных функций? Я бы не изобретал велосипед и разделил модели предсказания, которые работают по принципу классификатора или регрессии. Регрессионная предсказывает значение временного ряда, а модель классификации — возрастёт или уменьшится его значение в будущем временном промежутке.
Зависит ли российская экономика от цен на нефть?
Итак, ближе к делу давайти при помощи анализа временных рядов ответим на сакраментальный вопрос — зависит ли россиская экономика от цен на нефть. Одни (одна) говорят что нет, это миф, другие утверждают, что правда. Пусть данные говорят за нас. Сначала импортируем нужные модули:
# для загрузки данных import pandas_datareader.data as web # для анализа import numpy as np import pandas as pd import statsmodels.api as sm # для визуализации import matplotlib.pyplot as plt %config InlineBackend.figure_format = 'svg' plt.rcParams['figure.figsize'] = (10, 6)
Данные о ценнах на нефть марки Brent мы возьмём из базы данных федерального резерва США, а индикатором состояния российской экономики будет служить Индекс RTSI, рассчёт которого производится на основе 50 ликвидных акций крупнейших и динамично развивающихся российских эмитентов, виды экономической деятельности которых относятся к основным секторам экономики. Для загрузки данных будет использован модуль pandas_datareader, который позволяет импортировать данные из различных источников.
start = '2013-01-01' end = '2018-12-31' brent = web.DataReader('DCOILBRENTEU', 'fred', start=start, end=end) rsti = web.DataReader('RTSI', 'moex', start=start, end=end) rsti = rsti.query("BOARDID == 'RTSI'")["CLOSE"] # группируем по дням на всякий случай brent = brent.groupby(pd.Grouper(freq='1D')).aggregate("mean") rsti = rsti.groupby(pd.Grouper(freq='1D')).aggregate("mean") # приводим к одному виду brent.index.rename("date", inplace=True); brent = brent.iloc[:,0].rename("brent_price"); rsti.index.rename("date", inplace=True); rsti.rename("rsti_price", inplace=True); df = pd.DataFrame([rsti, brent]).T
Вначале произведём графический анализ этих двух временных рядов, отложив их на одном графике, но каждый по своей вертикальной оси (такое представление нивелирует различие в порядках величин).
plt.figure(figsize=(12,5)) plt.title('Индекс RSTI и цена на нефть') ax1 = df.rsti_price.plot(color='blue', grid=True, label='RSTI') ax2 = df.brent_price.plot(color='red', grid=True, secondary_y=True, label='Brent') h1, l1 = ax1.get_legend_handles_labels() h2, l2 = ax2.get_legend_handles_labels() plt.legend(h1+h2, l1+l2, loc=1) plt.show()
Похоже, определённые совпадения есть. Или нет. Нельзя сказать точно, пока не посчитаем корреляцию. Расчёт корреляции — это самый простой способ определить степень линейной связи двух числовых рядов (в том числе и временных).
# для расчёта корреляции необходимо удалить пропущенные значения corr = df.dropna().rsti_price.corr( df.dropna().brent_price ) "Correlation is {:.3}".format(corr)
Корреляция более 0.66 обычно считается сильной, а у нас целых 0.85. Можно ли этим удовлетвориться? Нет!
Применяя корреляция к значениями временного ряда вы будете стабильно получать её высокое значение. Это происходит потому что исходные значения временных рядов как правило нестационарны. Решением может быть использование для корреляции не исходные данные о ценах, а процентное изменение этих цен по сравнению с предыдущим шагом. О том, почему это работает, можно почитать здесь, здесь, здесь и здесь, а пока давайте рассчитаем корреляцию на процентном изменении цен.
pct_corr = df.dropna().rsti_price.pct_change().corr( df.dropna().brent_price.pct_change() ) "Percent change correlation is {:.3}".format(pct_corr)
И вот уже корреляция не такая уж и сильная.
Если мы построим график, в котором на одной оси отложим цену нефти, а на другом — индекс RST, то увидим, что во втором случае график более равномерный.
plt.subplot(1, 2, 1) plt.scatter( df.dropna().brent_price, df.dropna().rsti_price); plt.title('Correlation') plt.subplot(1, 2, 2) plt.scatter( df.dropna().rsti_price.pct_change(), df.dropna().brent_price.pct_change()); plt.title('Percent change correlation');
Степень линейной связи двух числовых рядов ещё можно устанвоить при помощи регрессионной модели, реализацию которой можно найти в том же пакете statsmodels, функции OLS. В качестве зависимой переменной укажем индекс RST, а на месте независимой — цену на нефть и свободный коэффициент, который заранее добавим фукнцией add_constant:
# Add a constant to the DataFrame x reg_def = sm.add_constant(df.dropna()) # Fit the regression of y on x result = sm.OLS(reg_def.rsti_price, reg_def[['const', 'brent_price']]).fit() # Print out the results result.summary()
| Dep. Variable: | rsti_price | R-squared: | 0.722 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.722 |
| Method: | Least Squares | F-statistic: | 3807. |
| Date: | Thu, 24 Jan 2019 | Prob (F-statistic): | 0.00 |
| Time: | 12:29:22 | Log-Likelihood: | -8987.6 |
| No. Observations: | 1469 | AIC: | 1.798e+04 |
| Df Residuals: | 1467 | BIC: | 1.799e+04 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 620.3612 | 8.452 | 73.397 | 0.000 | 603.782 | 636.941 |
| brent_price | 6.8799 | 0.112 | 61.699 | 0.000 | 6.661 | 7.099 |
| Omnibus: | 67.592 | Durbin-Watson: | 0.024 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 31.217 |
| Skew: | -0.132 | Prob(JB): | 1.67e-07 |
| Kurtosis: | 2.336 | Cond. No. | 223. |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Регрессионная модель показывает, что два временныз ряда значимо связаны (brent_price P>|t| < 0.05), причём цена на нефть объясняет 72.2% дисперсии индекса (R-squared: 0.722). Исходя из этого мы можем сказать, что связь между российской экономикой и ценой на нефть определённо есть.
Предсказание цены на нефть
Часто мы хотим предсказать цену основываясь лишь на её прошлых уровнях. Такой подход не самый точный, однако, во многих случаях его хватает для прогнозирования на приемлимом уровне. Давайте попробуем предсказать, какой будет цена на нефть через несколько месяцев. Для этого лучше увеличить масштаб данных и перейти от анализа данных за каждый день к ежемесячным наблюдениям при помощи метода resample:
df_monthly = df.resample('M').last() df_monthly.head()
| rsti_price | brent_price | |
|---|---|---|
| date | ||
| 2013-01-31 | 1622.13 | 115.55 |
| 2013-02-28 | 1534.41 | 112.20 |
| 2013-03-31 | 1460.04 | 108.46 |
| 2013-04-30 | 1407.21 | 101.53 |
| 2013-05-31 | 1331.43 | 100.43 |
Прежде, чем строить модели, необходимо узнать, а есть вообще в данном временном ряде связь между прошлыми и будущими его значениями. Если нет, вряд ли прогноз получится точным.
Определить степень связи между прошлыми и будущими значениями можно при помощи автокорреляции или, как её ещё называют, серийной коррелции (serial correlation) — эта та же корреляция, только рассчитывается она не между разными временными рядами, а на одном и том же, только с определённым сдвигом:
| Series | Laged Series |
|---|---|
| 1 | |
| 3 | 1 |
| 7 | 3 |
| 8 | 7 |
| 12 | 8 |
Если автокорреляция отрицательна, обычно говорят о тенденции временного ряда возвращаться к среднему уровню (mean reversion). Если положительна, то в дело вступает противоположная тенденция под названием моментум или следование тренду, когда котировки акций, которые повышаются или понижаются в данный период, скорее всего будут повышаться или понижаться в последующие периоды. Таким образом значение автокорреляции сигнализирует о необходимости выбора той или иной торговой стратегии.
"Price autocorr {:.3}, Percent Change autocorr {:.3}".format( df_monthly.brent_price.autocorr(), df_monthly.brent_price.pct_change().autocorr() )
Автокорреляция, посчитанная на изменение цены, в нашем случа не очень высокая, ниже, чем уровень, после которого принято говорить о наличии корреляции.
Однако, является ли эта корреляция статистически значимой? Сила корреляции и её значимость — это совсем не одно и то же. Сила корреляции показывает степень линейной связи, а её значимость говорит о том, что наблюдаемой значение отличается от 0 с определённый вероятностью (обычно более 95%). Простой способ посчитать границы доверительных интервалов — вычислить значение выражения , где N — количество наблюдений. Такая оценка работает только если автокорреляции при любых лагах равны 0.
Итак, мы нашли автокорреляцию первого порядка. Её может и не быть, но это лишь значит, что может присутствовать автокорреляция высших порядков. Под порядком в данном случае понимается тот самый лаг между значениями временного ряда. В нашем случае мы смотрели, связана ли цена на нефть с данном месяце с ценой за предыдущий месяц, и не нашли её. Если бы мы анализировали цену на зерно, то, скорее всего, пришли бы к похожим результатам. Цена на зерно, однако, отличается своей цезонностью — она низкая после сбора урожая ранней осенью и высокая после посевных работ, поэтому в этом случае корреляция прослеживалась бы каждый двенадцатый, двадцат четвёртый и т.д. месяц. Для того, чтобы выявить периодичность во временных рядах, используется функция автокорреляции — ACF, которая показывает значание автокорреляции для разных лагов.
График автокорреляций выборки в зависиости от сдвига называется коррелограммой, она проявляет неочевидные периодические составляющие сигнала. Построить коррелограмму можно при помощи модуля plot_acf библиотеки statsmodels. На графике также будет отобраён доверительный интервал, соответствующий уровню значимости .
from statsmodels.graphics.tsaplots import plot_acf from statsmodels.tsa.stattools import acf # для посчёта функции при разные значениях лага plot_acf(df_monthly.brent_price.diff().dropna());
Помимо ACF есть ещё PACF (частичная автокорреляционная фукнция), которая также показывает, значимо ли улучшение качества модели при увеличении её порядка. Для порядков, при которых значения PACF выходят за рамки доверительного интервала, можно говорить, о значительном приросте качества. Отличине в том, что в PACF рассчитывается только лишь корреляция между двумя переменных без влияния всех остальных.
Границы предсказания и стационарность временных рядов
Прежде, чем строить предсказательные модели, сделаем ещё одну заметку, касающуюся границ пресказания временных рядов. Значения многих временных рядов, например цен на акции, не предсказуемы, скольку завтрашняя цена акции обычно складывается из согдняшней цены + белый, т.е. случайный, шум. Такие процессы, при которых изменение на каждом шаге не зависит от предыдущих и от времени, описываются моделью случайного блуждания (random walk):
Случайное блуждание также может происходить со смещением. Если смещение положительное — мы видим восходящий тренд, состоящий из случайных блужданий, если отрицательное — нисходящий:
steps = np.random.normal(loc=-.1, size=500) # Generate 500 random steps P = 100 * np.cumsum(steps) # Simulate the stock price plt.plot(P) plt.title("Simulated Random Walk with Negative Drift")
Случайное блуждание на то и случайное, что его нельзя предсказать, лучшем предиктором для него будтет предыдущее значение. Как проверить, описывается ли временной ряд моделью случайного блуждания?
Самый простой способ — построить регрессионную модель, где в качестве зависимой переменной указать цену за период , а в качестве независимой — цену за период . Тогда если коэффициент в такой модели незаначимо отличается от 1, мы можем говорить о наличии случайного блуждания.
Другой способ проверить временной ряд на случайное блуждание — применить дополненный тест Дики — Фуллера (ADF-тест, augmented Dickey — Fuller test). Этот тест является одним из тестов на единичные корни (Unit root test), которые показывают, насколько сильно временной ряд определяется трендом. Нулевая гипотеза теста состоит в том, что временной ряд может быть представлен единичным корнем, который не является стационарным, а альтернативная, таким образом, в том, что временной ряд стационарен. Как всегда, если p-value < 0.05 мы отвергаем нулевую гипотезу.
from statsmodels.tsa.stattools import adfuller adfuller_p = adfuller(df_monthly['brent_price'])[1] f"p-value of ADF-test {adfuller_p:.3}"
Моделирование временных рядов регрессионными уравнениями
Разные регрессионным модели — это основной способ моделирования временных рядов. Самый популярная модель называется ARIMA — интегрированная модель авторегрессии — скользящего среднего (autoregressive integrated moving average). Есть множество других, более сложных и специализированных моделей, рифмующихся с ней: SARIMA, ARFIMA, VARMA и другие. Мы коснёмся и их, но вначале разберём три более простые модели — AR, MA и ARMA, которая является обобщением двух предыдущих.
Модель авторегрессии (AR, autoregression)
from statsmodels.tsa.arima_model import ARMA # Forecast the first AR(1) model mod = ARMA(df_monthly['rsti_price'].dropna(), order=(1, 0)); res = mod.fit(); res.summary()
| Dep. Variable: | rsti_price | No. Observations: | 72 |
|---|---|---|---|
| Model: | ARMA(1, 0) | Log Likelihood | -411.016 |
| Method: | css-mle | S.D. of innovations | 71.698 |
| Date: | Fri, 25 Jan 2019 | AIC | 828.031 |
| Time: | 16:56:02 | BIC | 834.861 |
| Sample: | 01-31-2013 | HQIC | 830.750 |
| - 12-31-2018 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 1198.8916 | 160.579 | 7.466 | 0.000 | 884.163 | 1513.620 |
| ar.L1.rsti_price | 0.9567 | 0.034 | 27.764 | 0.000 | 0.889 | 1.024 |
| Real | Imaginary | Modulus | Frequency | |
|---|---|---|---|---|
| AR.1 | 1.0452 | +0.0000j | 1.0452 | 0.0000 |
res.plot_predict(start=0, end="2019-06");
Выбор порядка авторегрессионной модели
Есть два простых способа определить порядок модели — 1) по короллерограмме PACF или ACF, 2) с использованием информационного критерия.
from statsmodels.graphics.tsaplots import plot_pacf plot_pacf(df_monthly['rsti_price'].dropna(), lags=20);
for order in range(1, 10): mod = ARMA(df_monthly['rsti_price'].dropna(), order=(order, 0)) res = mod.fit(); print("Order: {}\nBIC: {}\nAIC: {}\n".format(order, res.bic, res.aic))
BIC: 834.8611948102445
AIC: 828.0311964531963
Order: 2
BIC: 837.9148827514204
AIC: 828.8082182753561
Order: 3
BIC: 842.0576013951694
AIC: 830.6742708000892
Order: 4
BIC: 845.605006475491
AIC: 831.9450097613947
Order: 5
BIC: 849.3498930224819
AIC: 833.4132301893695
Order: 6
BIC: 853.5965991440432
AIC: 835.3832701919148
Order: 7
BIC: 857.7120524477489
AIC: 837.2220573766044
Order: 8
BIC: 857.0282329751997
AIC: 834.2615717850391
Order: 9
BIC: 850.4158859144329
AIC: 825.3725586052564
Модель скользящего среднего, Moving Average (MA)
Согласно модели скользящего среднего актуальное значение целевой переменной складывается с средней величины и суммы случайных ошибок за прошлые периоды с некоторыми их весами.
В общем виде формула модели скользящей средней порядка (то есть учитывающая временных периодов) выглядит как сумма произведений значений за предыдущие периоды на веса этих значений:
где — это ошибка, белый шум, — вес шума за определённый период модели ( можно считать равным без ограничения общности).
Таким образом, модель скользящего среднего значения по сути представляет собой линейную регрессию, где актуальное значение временного ряда зависит от величины белого шума в текущем периоде и предыдущих.
Рассмотрим подробнее модель первого порядка, которая будет выглядить следующим образом:
Если параметр равен нулю, мы получаем обычный белый шум — модель скользящей средней нулевого порядка MA(0).
Если параметр меньше 0, то мы можем говорить о тенденции временного ряда возвращаться к среднему уровню (Mean Reversion), поскольку ошибка за текущий период будет компенсироваться ошибкой за прошлый период. Если же параметр больше 0, мы можем говорить о моментум.
Сгенерировать временной ряд с нужными свойствами можно при помощи функции ArmaProcess. Далее мы сгенерируем два временных ряда, чтобы параметр модели скользяцего среднего первого порядка был равен в первом случае и во втором.
# import the module for simulating data from statsmodels.tsa.arima_process import ArmaProcess # Plot 1: MA parameter = -1 plt.subplot(2,1,1) ar1 = np.array([1]) ma1 = np.array([1, -1]) MA_object1 = ArmaProcess(ar1, ma1) simulated_data_1 = MA_object1.generate_sample(nsample=1000) plt.plot(simulated_data_1) # Plot 2: MA parameter = 1 plt.subplot(2,1,2) ar2 = np.array([1]) ma2 = np.array([1, 1]) MA_object2 = ArmaProcess(ar2, ma2) simulated_data_2 = MA_object2.generate_sample(nsample=1000) plt.plot(simulated_data_2)
В отличие от авторегрессионной модели -ого порядка, модель скользящего среднего -ого порядка практически не имеет автокорреляции далее этого порядка
# Import the plot_acf module from statsmodels from statsmodels.graphics.tsaplots import plot_acf # Plot three ACF on same page for comparison using subplots fig, axes = plt.subplots(2,1) # Plot 1: AR parameter = -0.9 plot_acf(simulated_data_1, lags=20, ax=axes[0]) axes[0].set_title("MA Parameter -0.9") # Plot 2: AR parameter = +0.9 plot_acf(simulated_data_2, lags=20, ax=axes[1]) axes[1].set_title("MA Parameter +0.9")
Моделировать модешь MA можно при помощи той же функции ARMA, что и модель AR, надо лишь указать её порядок у второго элемента в последовательности, передеваемой аргументу order.
ARMA(df_monthly['rsti_price'].dropna(), order=(0, 1)
ARMA
Как видно из названия, ARMA — это комбинация моделей AR и MA, поэтому её формулы выглядит так:
Коинтеграционные модели
Иногда временные ряды связаны — изменение в одном приводит к предсказуемому изменению в другом. Такое часто случаяется с ценами на товары-заменители, например, нефть и газ. Из экономической теории мы знаем, что рост цены на одни товары-заменители проводит к росту потребления других, что, в свою очередь, также приводит к росту цен на них. Например, автомобили обычно работают на бензине, который делается из нефти, но многие также могут работать и на газу при несложном апгрейде. Таким образом, если цена на нефть повышается, цена на на газ также непременно повысится через некоторое время (обычно, полгода). Поэтому, даже если два временных ряда совершенно не прогнозируемы исходя из своей истории, они могут быть предсказаны с опорой на другие временные ряды при помощи так нызваемых коинтеграционных моделей. Под коинтеграцией понимается причинно-следственная зависимость в уровнях двух (или более) временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и случайной колеблемости.
Для того, чтобы понять, насколько один временной ряд () может быть предсказан с помощью другого (), нужно вначале построить регрессионную модель со значениями первого ряда в качестве зависимой переменной. Угловой коэффициент () в этой регрессионной модели будет показывать силу данной связи. Затем необходимо запустить дополненный тест Дики — Фуллера (ADF), о котором мы говорили ранее, на линейной комбинации двух временных рядов, рассчитанной как . Оба этих шага реализованы в функции coint модуля statsmodels.tsa.stattools.
Давайте проверим гипотезу о связи газа и нефти на практике. Для этого вначале загрузим данные о цене на природный газ с газового хаба Henry Hub, который играет ведущую роль в формировании цен на природный газ в США, поскольку он является точкой доставки для спотовых и фьючерсных контрактов на природный газ, торгуемых на Нью-Йоркской товарно-сырьевой бирже (NYMEX) и Межконтинентальной бирже (ICE). Источником данных будет служить сайт Федерального резерва США.
gas = web.DataReader('MHHNGSP', 'fred', start, end) df_monthly["gas"] = gas.resample('M').last()
Далее построим график, показывающий взаимное изменение цены на нефть и газ:
plt.plot(df_monthly.brent_price, label='Brent Oil') plt.plot(df_monthly.gas * 20, label='Natural Gas');
Видно, что некоторая связь есть. Можно приступать к следующему шагу — построению регрессионной модели и определению угового коэффициента, на который надо домножить цену на раз, чтобы она стала одного порядка с ценой на нефть.
reg_def = sm.add_constant(df_monthly.dropna()) result = sm.OLS(reg_def['brent_price'], reg_def[['gas']]).fit() result.params.gas
Видим, что после проведения этих манипуляций временной ряд стал похож на стационарный.
# Plot the prices separately plt.subplot(2,1,1) plt.plot(df_monthly.brent_price, label='Brent Oil') plt.plot(df_monthly.gas * result.params.gas, label='Natural Gas') plt.legend(loc='best', fontsize='small') # Plot the spread plt.subplot(2,1,2) plt.plot(df_monthly.brent_price - df_monthly.gas * result.params.gas, label="Spread") plt.legend(loc='best', fontsize='small') plt.axhline(y=0, linestyle='--', color='k');
Проверим, действительно ли у нас получился стационарный ряд из двух нестационарных. Используем для этого упоминавшийся ранее дополненный тест Дики — Фуллера.
from statsmodels.tsa.stattools import adfuller result_oil = adfuller(df_monthly['brent_price']) result_gas = adfuller(df_monthly['gas']) print(f"The p-value for the ADF test on oil is {result_oil[1]:.2}, on gas is {result_gas[1]:.2}") result_spread = adfuller(df_monthly.brent_price - df_monthly.gas * result.params.gas) print(f"The p-value for the ADF test on the spread is {result_spread[1]:.2}")
The p-value for the ADF test on the spread is 0.047
ARIMA
Модели авторегрессии и скользящего среднего строятся исходя из условия стационарности. Стационарный процесс в сильном смысле — это процесс, в котором распределение случайной величины не изменяется со временем, а в слабом — это процесс с постоянным математическим ожиданием и дисперсией, в котором ковариация между значениями ряда зависит только от величины лага.
Условие стационарности для моделей ARMA связано с идеей, лежащей в основе модели линейного фильтра, на которой базируется ARMA: временнóй ряд рассматривается как генерируемый под влиянием ряда независимых случайных ошибок (шумов, шоков), имеющих некое фиксированное распределение (обычно нормальное). Согласно этой идее случайные шоки проходят через фильтр (в роли которого выступает модель ARMA), на выходе которого получаются значения ряда . Для моделирования технических процессов такая модель работает, но социально-экономические процессы, конечно же, значительно более разнообразны, а поэтому и нестационарность в них встречается значительно чаще.
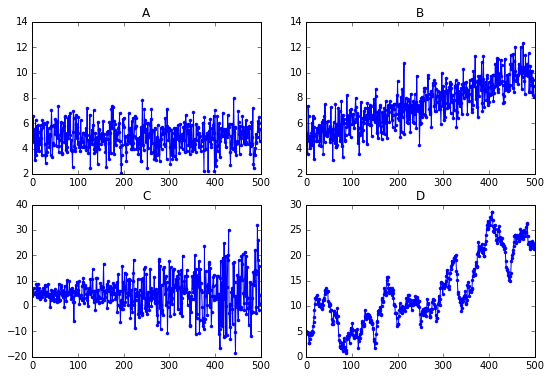
Как стабилизировать временные ряды? Помните, как ранее мы считали корреляцию на данных о процентном измененинии цены и говорили, что такие результаты более стабильны, покольку временной ряд становится более стационарным? Тут идея также самая — мы стоим модель на основе разностей значения за последующих периодов. Модель авторегрессии со скользящей средней, построенная на основе разностей, обозначается как , где буква отвечает за порядок интеграции (взятой разности).
Обычно при построении модели ARIMA порядок разностей ограничивается числом . Это вызвано тем, что взятие вторых разностей обычно позволяет привести к стационарному виду практически любые нестационарные ряды данных.
sber = web.DataReader('SBER', 'moex', start='16-06-2017', end='22-02-2018')
sber = sber.query("BOARDID == 'TQBR'").CLOSE.resample("W").last() sber.plot()
plot_acf(sber, lags=20);
from statsmodels.tsa.arima_model import ARIMA model = ARIMA(sber, order=(5,1,0)); model_fit = model.fit(); model_fit.summary()
Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
/usr/local/lib/python3.7/site-packages/scipy/signal/signaltools.py:1344: FutureWarning:
Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
/usr/local/lib/python3.7/site-packages/scipy/signal/signaltools.py:1350: FutureWarning:
Using a non-tuple sequence for multidimensional indexing is deprecated; use `arr[tuple(seq)]` instead of `arr[seq]`. In the future this will be interpreted as an array index, `arr[np.array(seq)]`, which will result either in an error or a different result.
| Dep. Variable: | D.CLOSE | No. Observations: | 35 |
|---|---|---|---|
| Model: | ARIMA(5, 1, 0) | Log Likelihood | -111.658 |
| Method: | css-mle | S.D. of innovations | 5.823 |
| Date: | Fri, 25 Jan 2019 | AIC | 237.316 |
| Time: | 02:11:48 | BIC | 248.203 |
| Sample: | 07-02-2017 | HQIC | 241.074 |
| - 02-25-2018 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 3.5598 | 0.493 | 7.220 | 0.000 | 2.593 | 4.526 |
| ar.L1.D.CLOSE | -0.2194 | 0.166 | -1.318 | 0.198 | -0.546 | 0.107 |
| ar.L2.D.CLOSE | -0.2623 | 0.181 | -1.448 | 0.158 | -0.617 | 0.093 |
| ar.L3.D.CLOSE | -0.2375 | 0.179 | -1.326 | 0.195 | -0.589 | 0.114 |
| ar.L4.D.CLOSE | -0.0900 | 0.183 | -0.492 | 0.627 | -0.449 | 0.269 |
| ar.L5.D.CLOSE | -0.3064 | 0.177 | -1.736 | 0.093 | -0.652 | 0.040 |
| Real | Imaginary | Modulus | Frequency | |
|---|---|---|---|---|
| AR.1 | 0.8537 | -0.9421j | 1.2714 | -0.1328 |
| AR.2 | 0.8537 | +0.9421j | 1.2714 | 0.1328 |
| AR.3 | -1.2380 | -0.0000j | 1.2380 | -0.5000 |
| AR.4 | -0.3816 | -1.2187j | 1.2770 | -0.2983 |
| AR.5 | -0.3816 | +1.2187j | 1.2770 | 0.2983 |
Вначале, выведем ошибки на графике. Если модель вобрала в себя все информацию о тренде, график должен выглядеть как белый шум — это хороший знак.
residuals = pd.DataFrame(model_fit.resid) residuals.plot()
model_fit.plot_predict(end="22-04-2018");
Интегрирование — не единственный инструмент по приведению нестационарного ряда к стационарному виду.
Наверное, самый просто метод получения постоянной дисперсии — логарифмирование исходного ряда данных. Он позволяет получить ряд с постоянной дисперсией в тех случаях, когда ошибка в модели носит мультипликативный характер (что приводит к тому, что с ростом уровня ряда растет и дисперсия ошибки).
Другой простой метод приведения к стационарности — это построение по исходному ряду данных модели тренда. Построив модель выбранного тренда, исследователь рассчитывает остатки по модели и уже по ним строит модель ARMA.
Ещё один способ способ — описать исходный ряд данных нестационарной моделью AR, после чего по полученным остаткам построить модель ARMA. Полученная в итоге модель называется ARARMA [5].
Еще одним вариантом приведения ряда данных к стационарному виду является взятие нецелых разностей (когда становится нецелым числом), что достигается путем их разложения в ряды Тейлора. Суть метода заключается в том, что взятие целых разностей может быть излишним для ряда данных (стационарность может лежать где-то между и ). Порядок разности в таком случае подбирается автоматически. По преобразованному ряду вновь строится ARMA. Модель, получаемая в результате этого, носит название ARFIMA (AutoRegressive Fractionally Integrated Moving Average).
Сезонность во временных рядах
Сезонность — это некоторый повторяющийся паттерн, наблюдаемый во временных рядах. Например, количество автопроишествий каждый год увеличивается с наступлением зимы, как и количество аварий в сфере ЖКХ; цены на овощи снижаются летом и возрастаю зимов, когда буквально «не сезон», а количество обращений в шиномонтаж увеличивается весной и осенью и т.д. Выявить сезонность проще всего при помощи функции автокорреляции — в аналогичные периоды других сезонов коррелелограмма будет показывать заметно более высокие значения автокорреляции.
Сезонные колебания надо постараться учесть в модели, иначе её предсказания будут действовать только до конца сезона. Если разные способы это сделать. Можно трансформировать данные (seasonal adjustment) или использовать специально предназначенные для этого модели — SARIMA.
Возьмем в качестве примера временной ряд, где вполне возможно ожидать сезонность — цену на килограмм яблок в России — определим, действительно в нём имеется сезонный компонент, а затем построим прогноз при помощи модели SARIMA. Цену на яблоки и другие товары можно узнать га сайте РосСтата.
apples = pd.read_csv("http://nagornyy.me/datasets/apples_gks.csv", sep=";", encoding="cp1251", header=1) apples.head()
| Unnamed: 0 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | Unnamed: 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 01 неделя (на 11 января) | 65,77 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1 | 02 неделя (на 17 января) | 66,54 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 2 | 03 неделя (на 24 января) | 67,59 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3 | 04 неделя (на 31 января) | 68,21 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 4 | 05 неделя (на 7 февраля) | 69,01 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
Подготовим данные и построим график:
dateindex = pd.date_range(start='01-10-2011', periods=len(apples), freq='7D') apples.index = dateindex season = pd.Series(index=dateindex) for year in range(2011, 2019): season = season.fillna(pd.to_numeric(apples[str(year)].str.replace(",", "."))) season.plot(title="Цены на яблоки по неделям", grid=True);
Построим короллелограмму и посмотрим, есть ли периоды, когда кореляция намного выше. Поскольку сезон длится 3 месяца, укрупним данные.
plot_acf(season.resample("3M").last().diff().dropna());
Определённо сезонность присутвует — мы наблюдаем корреляция с лагом каждые четыре шага.
Можно легко её устранить, продифференцировав временной ряд вручную.
plot_acf(season.resample("3M").last().diff(4).dropna());
Определить наличие сезонности можно также при помощи функции seasonal_decompose пакета statsmodels, которая разложит временной ряд на три компонента — трендовый, сезонный и всё остальное по оригинальному методу 1920-х годов [6].
from statsmodels.tsa.seasonal import seasonal_decompose result = seasonal_decompose(season.resample("3M").last(), model='additive') result.plot();
SARIMA
Для построения авторегрессионной модели на временных рядах с присутствием сезонного компонента используется расширение очередное расширение модели ARIMA — SARIMA, где S означает seasonal. В общем виде модель выглядит так: где — старые параметры пришедщие из ARIMA, а (P,D,Q)s — группа новых параметров, специфичных для SARIMA. Они задают, насколько сезонов мы смотрим назад, когда её предсказываем. Рассмотрим каждый параметр подробнее.
- - порядок модели ;
- - порядок интегрирования;
- - порядок модели
- - порядок сезонной составляющей ;
- - порядок интегрирования сезонной составляющей;
- - порядок сезонной составляющей ;
- — размерность сезонности.
Имплементация этой модели также есть в библиотеке statsmodels [7], так что ей и воспользуемся.
from statsmodels.tsa.statespace.sarimax import SARIMAX order = (1, 1, 1) seasonal_order = (1, 1, 1, 4) model = SARIMAX(season.resample("3M").last(), order=order, seasonal_order=seasonal_order) res = model.fit()
df = pd.DataFrame() df['past'] = season.resample("3M").last().append(res.forecast(10)) df['future'] = res.forecast(10)
df.plot();
На этом мы закончили в прогнозированием временны рядов при помощи регресиионных уравнений. Для интересующихся этой темой могу посоветовать хороший курс по анализу временных рядов на Coursera: Practical Time Series Analysis.
Самостоятельная работа
Спрогнозируйте цену потребительского товара, в котором, на ваш взгляд, может присутствовать сезонность. Для этого надо: 1) выбрать товар и загрузить историю изменения его цены, 2) определить наличие сезонности или её отсутствие, 3) выбрать подходящую модель и построить прогноз на несколько месяцев с её помощью.
Анализ аудио записей
Как говорилось взначале — аудио-записи тоже относятся к временным рядам, ведь звук представляет собой непрерывный сигнал — звуковую волну с меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче, а чем больше частота сигнала, тем выше тон.
Далее мы будем работать со звуком и построим классификатор, которые будет определять наличие проблем с сердцем по звуку его биения. Данные были взяты с соревнования на Kaagle, код частично позаимствовал с курса на Datacamp, так что можете пройти его для повторения.
Первое, что вам нужно сделать — это загрузить данные со страницы соревнования на Kaggle. Распакуйте их на себе на компьютер, а затем, при помощи библиотеки librosa загрузите первый аудиофайл в память и визаулизируйте звуковую волну.
import librosa as lr from glob import glob # List all the wav files in the folder audio_files = glob('http://nagornyy.me/datasets/heartbeat-sounds/set_a' + '/*.wav') # Read in the first audio file, create the time array audio, sfreq = lr.load(audio_files[0]) time = np.arange(0, len(audio)) / sfreq # Plot audio over time fig, ax = plt.subplots() ax.plot(time, audio) ax.set(xlabel='Time (s)', ylabel='Sound Amplitude')
Похоже на правду. Теперь можно загружать и остальные файлы с их мета-информацией, которая хранится в файле set_a.csv.
heart_meta = pd.read_csv("http://nagornyy.me/static/datasets/heartbeat-sounds/set_a.csv") heart_meta.head()
| dataset | fname | label | sublabel | |
|---|---|---|---|---|
| 0 | a | set_a/artifact__201012172012.wav | artifact | NaN |
| 1 | a | set_a/artifact__201105040918.wav | artifact | NaN |
| 2 | a | set_a/artifact__201105041959.wav | artifact | NaN |
| 3 | a | set_a/artifact__201105051017.wav | artifact | NaN |
| 4 | a | set_a/artifact__201105060108.wav | artifact | NaN |
В столбце label содержится информация о типе проблемы или её отсутствии (normal).
heart_meta.label.value_counts()
murmur 34
normal 31
extrahls 19
Name: label, dtype: int64
В учебных целях построим классификатор, которые определяет недуг по загадочным названием murmur 🐱. Далее будет идти не очень вразумительный код, написанный впопыхах.
norm_sample = heart_meta[heart_meta.label == "normal"] murmur_sample = heart_meta[heart_meta.label == "murmur"] df_norm = pd.DataFrame() for id, fname in norm_sample.fname.iteritems(): path = "http://nagornyy.me/datasets/heartbeat-sounds/" + fname audio, sfreq = lr.load(path) time = np.arange(0, len(audio)) / sfreq s = pd.Series(data=audio, index=time) df_norm[fname] = s df_murmur = pd.DataFrame() for id, fname in murmur_sample.fname.iteritems(): path = "http://nagornyy.me/datasets/heartbeat-sounds/" + fname audio, sfreq = lr.load(path) time = np.arange(0, len(audio)) / sfreq s = pd.Series(data=audio, index=time) df_murmur[fname] = s df = pd.concat([df_norm, df_murmur], axis=1, sort=False) df.head()
| set_a/normal__201101070538.wav | set_a/normal__201101151127.wav | set_a/normal__201102081152.wav | set_a/normal__201102081321.wav | set_a/normal__201102201230.wav | set_a/normal__201102260502.wav | set_a/normal__201102270940.wav | set_a/normal__201103090635.wav | set_a/normal__201103101140.wav | set_a/normal__201103140132.wav | ... | set_a/murmur__201108222243.wav | set_a/murmur__201108222245.wav | set_a/murmur__201108222246.wav | set_a/murmur__201108222248.wav | set_a/murmur__201108222251.wav | set_a/murmur__201108222252.wav | set_a/murmur__201108222253.wav | set_a/murmur__201108222255.wav | set_a/murmur__201108222256.wav | set_a/murmur__201108222258.wav | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.000000 | 0.000372 | 0.030530 | 0.003224 | 0.006436 | 0.000222 | -0.010349 | -0.000554 | 0.000525 | -0.000053 | 0.000152 | ... | -0.006913 | -0.185096 | -0.031637 | -0.000614 | -0.013211 | 0.113057 | -0.168317 | 0.004103 | -0.102160 | 0.010673 |
| 0.000045 | 0.000374 | 0.044925 | 0.006052 | 0.008510 | 0.000273 | -0.015578 | -0.000925 | 0.000365 | 0.000022 | 0.000045 | ... | -0.011213 | -0.296707 | -0.050700 | -0.000937 | -0.021293 | 0.181618 | -0.270060 | 0.006612 | -0.164134 | 0.017101 |
| 0.000091 | 0.000043 | 0.039490 | 0.003248 | 0.004068 | -0.000385 | -0.014346 | -0.000357 | 0.000415 | -0.000021 | -0.000105 | ... | -0.010705 | -0.280282 | -0.047796 | -0.000852 | -0.020425 | 0.172172 | -0.255433 | 0.006415 | -0.155556 | 0.016136 |
| 0.000136 | 0.000183 | 0.042998 | 0.006324 | 0.001876 | -0.000176 | -0.015706 | 0.000178 | 0.000907 | -0.000013 | -0.000057 | ... | -0.011455 | -0.299051 | -0.050911 | -0.000864 | -0.022089 | 0.184313 | -0.272905 | 0.006997 | -0.166525 | 0.017117 |
| 0.000181 | 0.000044 | 0.040716 | 0.004714 | -0.001555 | -0.000049 | -0.014963 | 0.000268 | 0.000819 | -0.000087 | -0.000092 | ... | -0.010570 | -0.273499 | -0.046451 | -0.000738 | -0.020629 | 0.169395 | -0.249984 | 0.006671 | -0.153068 | 0.015494 |
5 rows × 65 columns
df.iloc[:, :3].plot(subplots=True, layout=(3,1));
df.iloc[:, -3:].plot(subplots=True, layout=(3,1));
mean_normal = np.mean(df_norm, axis=1) mean_abnormal = np.mean(df_murmur, axis=1) # Plot each average over time fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3), sharey=True) ax1.plot(df_norm.index, mean_normal) ax1.set(title="Normal Data") ax2.plot(df_murmur.index, mean_abnormal) ax2.set(title="Abnormal Data");
mean.shape
mean = pd.concat([mean_normal, mean_abnormal]) df_agg = pd.DataFrame() df_agg["mean"] = mean df_agg["label"] = pd.Series(data = [0]*len(mean_normal) + [1]*len(mean_abnormal), index=df_agg.index) df_agg.head()
| mean | label | |
|---|---|---|
| 0.000000 | -0.015229 | 0 |
| 0.000045 | -0.022219 | 0 |
| 0.000091 | -0.019271 | 0 |
| 0.000136 | -0.020672 | 0 |
| 0.000181 | -0.019303 | 0 |
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( df_agg[["mean"]], df_agg.label, test_size=0.2, random_state=12)
from sklearn.svm import LinearSVC model = LinearSVC() model.fit(X_train, y_train);
from sklearn.metrics import accuracy_score predictions = model.predict(X_test) accuracy_score(predictions, y_test)
df_rectified = df.apply(np.abs) df_rectified.iloc[:, 0].plot();
df_rectified_smooth = df_norm_rectified.rolling(500).mean() df_rectified_smooth.iloc[:, 0].plot();
means = np.mean(df_rectified_smooth, axis=0) stds = np.std(df_rectified_smooth, axis=0) maxs = np.max(df_rectified_smooth, axis=0) # Create the X and y arrays X = np.column_stack([means, stds, maxs]) y = df_rectified.columns.str.contains("murmur").astype(int) # Fit the model and score on testing data from sklearn.model_selection import cross_val_score percent_score = cross_val_score(model, X, y, cv=5) print(np.mean(percent_score))
Самостоятельная работа
Посмотрите видео The spectrogram курса Machine Learning for Time Series Data in Python. Следуйте инструкциям на видео и постройте спектограмму временного ряда. Сгенерируйте признаки из спектограммы (spectral bandwidth и spectral centroid) и примените их в модели.
Комментарии