Как думаете, вес какого признака будет наибольшим?
История вычислительных нейронных сетей
Как всё начиналось: Нейрон Маккалока-Питтса
Термин «нейронная сеть» появился в середине XX века. Первые работы, в которых были получены основные результаты в данном направлении, были проделаны Мак-Каллоком и Питтсом [1]. В 1943 году ими была разработана модель нейронной сети на основе математических алгоритмов и теории деятельности головного мозга. Давайте почитаем, как они описывают деятельность головного мозга. Многое из этого актуально и сейчас.
Theoretical neurophysiology rests on certain cardinal assumptions. The nervous system is a net of neurons, each having a soma and an axon. Their adjunctions, or synapses, are always between the axon of one neuron and the soma of another. At any instant a neuron has some threshold, which excitation must exceed to initiate an impulse. This, except for the fact and the time of its occurrence, is determined by the neuron, not by the excitation. From the point of excitation the impulse is propagated to all parts of the neuron. The velocity along the axon varies directly with its diameter, from less than one meter per second in thin axons, which are usually short, to more than 150 meters per second in thick axons, which are usually long. The time for axonal conduction is consequently of little importance in determining the time of arrival of impulses at points unequally remote from the same source. Excitation across synapses occurs predominantly from axonal terminations to somata.
В переводе на язык картинок, модель нейрона по этому описанию выглядит так:
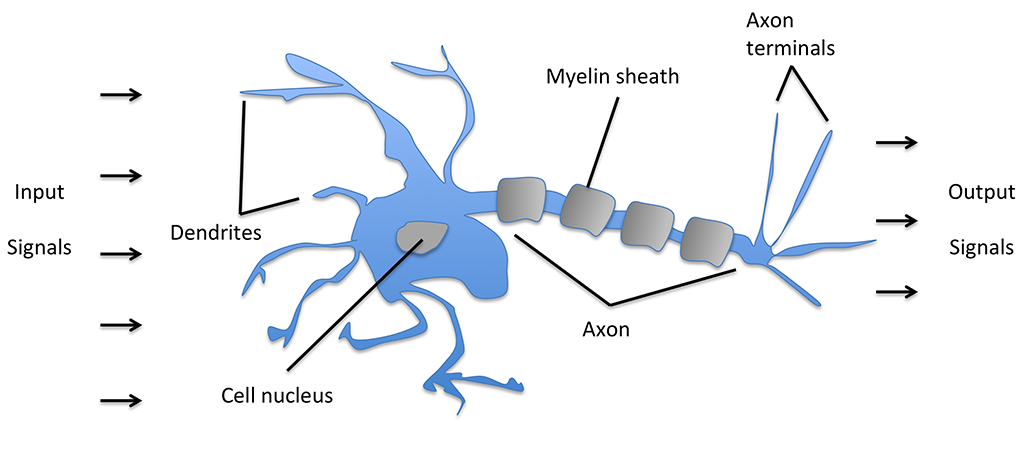
Тогда они делают вывод:
и описывают математическую модель искусственного нейрона в виде простого логического элемента с бинарными выходами; множественные входные сигналы поступают в дендриты, затем интегрируются в клеточное тело, и если накопленный сигнал превышает определенный порог, то генерируется выходной сигнал, который аксоном передается дальше.Because of the "all-or-none" character of nervous activity, neural events and the relations among them can be treated by means of propositional logic. It is found that the behavior of every net can be described in these terms, with the addition of more complicated logical means for nets containing circles; and that for any logical expression satisfying certain conditions, one can find a net behaving in the fashion it describes.
Перцептрон Розенблата
В 1958 г. на основе нейрона Маккалока-Питтса Фрэнк Розенблатт представил научному сообществу концепцию правила обучения персептрона [2]. Вместе с правилом персептрона Розенблатт предложил алгоритм, который автоматически обучался оптимальным весовым коэффициентам, которые затем перемножались с входными признаками для принятия решения о том, активировать нейрон или нет. В контексте обучения с учителем и задачи классификации такой алгоритм можно использовать для распознавания принадлежности образца к тому или иному классу.
Розенблат очень верил в свою модель и активно её популяризировал. Уже тогда говорилось, что при помощи перцептрона можно будет делать множество крутых вещей, например, классифицировать изображения. Как вы помните, именно в это время человек начал покорять космос, активно развивалась научная фантасткика, общественность грезила . Благодаря этому оптимизм Розенблата попал на удобренную почву — о перцептроне заговорили, да её как. Чтобы понять уровень хайпа вокруг перцептрона, почитайте эта статью из NYT, где читателям опещали уже совсем скоро изобрести скайнет:


Всё это кажется ещё более странно, если взглянуть на устройство этого перцптрона, который, как сейчас видится, был довольно простой модификацией логистической регресии, неспособной решить многие их тех проблем, на которые покушался Розенблат. Как окажется в дальнейшем, после массовой веры в мощь перцептрона пришло отрезвление, которое затормозило исследования в этой области на многие годы [3].
AI winter
В 1969 г. бывший сокурсник Розенблатта Марвин Минский и Сеймур Паперт опубликовали книгу «Перцептроны» [4], в которой привели строгое математическое доказательство того, что перцептрон не способен к обучению в большинстве интересных для применения случаев.

Устройство перцептрона Розенблата
Итак, перцептрон Розенблатта является линейной моделю бинарной классификации. Предположим, у на есть два класса: и или, для наглядности, 🐹хомячки и 🐼панды. Необходимо построить функцию, которая бы присваивала каждому объекту, описываемому N признаками, какой-то из двух классов. Для этого необходим вектор числовых значений признака и вектор весов, показывающих их важность для успешной классификации .
Предположим, у нас есть три основных признака, по которым мы можем отличать хомячков и панд друг от друга — вес, округлость и пушстость (в реальности число таких признаков может достигать сотен тысяч).
x^T×w = \begin{bmatrix} вес: & x_{1} \\ округлость: & x_{2} \\ пушистость: & x_{3} \end{bmatrix}^T × \begin{bmatrix} вес: & w_{1} \\ округлость: & w_{2} \\ пушистость: & w_{3} \end{bmatrix}
Далее перемножим значения признаков на их веса и суммируем, получив здесь называется сумматором или сумматорной функцией — это взвешенная сумма входов + смещение.
Смещение (англ. bias) — это та самая граница, после превышения которой нейрон активируется. Именно поэтмоу количество весов на самом деле на один больше, чем количество признаков — мы хотим настраивать эту границу, придавай ей определённый вес. Для приведения длинн векторов весов и признаков к одному виду мы просто добавляем 1 в начало вектора признаков.
Итак, мы получили некоторое значение сумматора. Необходимо решить, нужно ли активировать нейрон при таком значении, другими словами, можем ли мы сделать вывод о принадлежности объёкта к классу . Это решение на себя берёт функция активации . Если активация отдельно взятого образца , т. е. выход из , превышает заданный порог (это то самое смещение, о котором мы говорили ранее), то мы присваиваем класс , в противном случае . В этой модели функция активации также является и функцией потерь, т.е. функцией, которая оценивает, насколько хороша наша модель предсказывает данные.
В алгоритме персептрона функция активации - это простая ступенчатая функция, которую иногда также называют ступенчатой функцией Хевисайда (или функцией единичного скачка). \phi(z)= \begin{cases} 1, если \sum_{i=1}^n w_i×x_i \geq b \\ -1 \ иначе. \end{cases}
Налицо аналогия с естественными нейронами — если z первышает некий заданный порог, то нейрон активируется. В современный нейронных сетях чаще всего используют другие функции активации [5].
Наша задача — сделать так, чтобы нейрон активировался только тогда, когда это нужно. Для этого нам нужно подобрать оптимальные веса (и смещение, которое тоже можно считать весом фиктивного признака), ведь изначально они инициализируются нулями или случайными числами. Как это сделать?
Вычислем значение , которое надо будет прибавить к весу признака для улучшения предсказания: где — темп обучения от 0 до 1, - истинная метка класса для -ого примера, — его предсказанная метка класса.
Понятно, что если предсказанное значение совпало с фактическим, будет равно — веса в порядке. Если предсказанный класс, например, , а действительный , то будет равно некоторому положительному числу , прибавив которое к прошлому весу мы скорректируем предсказание в нужную сторону. Таким образом, всё, что нам нужно, это обновить веса, прибавив к их старым значенмиям:
Рассчёт весов на конкретном примере.
В двух сценариях, где персептрон правильно распознает метку класса, веса остаются неизменными: Однако в случае неправильного распознавания веса продвигаются в направлении соответственно положительного или отрицательного целевого класса:Графически модель можно представить так:
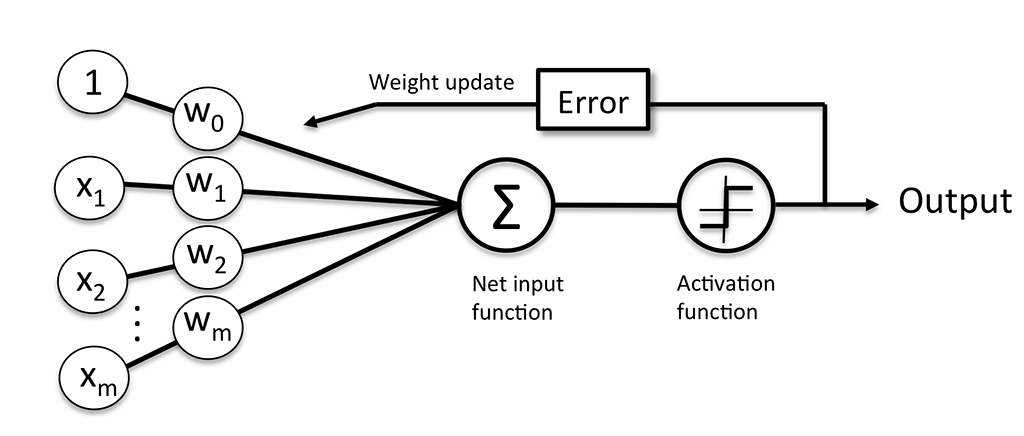
На этом почти все. Но прежде чем удивляться, как на такую простую модель можно было возлагать большие надежны, стоит знать, что Розенблатт предоплагал использовать не один перцептрон, а сети из их большого количества. К сожалению, это было сложно выполнимо с учётом ограниченных вычислительных мощностей того времени.
Реализация перцептрона Розенблата на Python
Давайте реализуем персептрон Розенблатта на Python [6], после чего применим его к известнейшему набору данных цветков ириса.
class Perceptron(object): """Perceptron classifier. Parameters ------------ eta : float Learning rate (between 0.0 and 1.0) n_iter : int Passes over the training dataset. shuffle : bool (default: True) Shuffles training data every epoch if True to prevent cycles. random_state : int (default: None) Set random state for shuffling and initializing the weights. Attributes ----------- w_ : 1d-array Weights after fitting. errors_ : list Number of misclassifications in every epoch. """ def __init__(self, eta=0.01, n_iter=10, shuffle=True, random_state=None): self.eta = eta self.n_iter = n_iter self.shuffle = shuffle if random_state: np.random.seed(random_state) def fit(self, X, y): """Fit training data. Parameters ---------- X : {array-like}, shape = [n_samples, n_features] Training vectors, where n_samples is the number of samples and n_features is the number of features. y : array-like, shape = [n_samples] Target values. Returns ------- self : object """ self.w_ = np.zeros(1 + X.shape[1]) self.errors_ = [] for _ in range(self.n_iter): if self.shuffle: X, y = self._shuffle(X, y) errors = 0 for xi, target in zip(X, y): update = self.eta * (target - self.predict(xi)) self.w_[1:] += update * xi self.w_[0] += update errors += int(update != 0.0) self.errors_.append(errors) return self def _shuffle(self, X, y): """Shuffle training data""" r = np.random.permutation(len(y)) return X[r], y[r] def net_input(self, X): """Calculate net input""" return np.dot(X, self.w_[1:]) + self.w_[0] def predict(self, X): """Return class label after unit step""" return np.where(self.net_input(X) >= 0.0, 1, -1)
import pandas as pd url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data' df = pd.read_csv(url, header=None, encoding="utf8") df.tail()
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | Iris-virginica |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | Iris-virginica |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | Iris-virginica |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | Iris-virginica |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | Iris-virginica |
%matplotlib inline %config InlineBackend.figure_format = 'svg' import matplotlib.pyplot as plt import numpy as np # select setosa and versicolor y = df.iloc[0:100, 4].values y = np.where(y == 'Iris-setosa', -1, 1) # extract sepal length and petal length X = df.iloc[0:100, [0, 2]].values # plot data plt.scatter(X[:50, 0], X[:50, 1], color='red', marker='o', label='setosa') plt.scatter(X[50:100, 0], X[50:100, 1], color='blue', marker='x', label='versicolor') plt.xlabel('sepal length [cm]') plt.ylabel('petal length [cm]') plt.legend(loc='upper left') plt.tight_layout() plt.show()
ppn = Perceptron(eta=0.1, n_iter=10) ppn.fit(X, y) plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o') plt.xlabel('Epochs') plt.ylabel('Number of updates') plt.tight_layout() plt.show()
from matplotlib.colors import ListedColormap def plot_decision_regions(X, y, classifier, resolution=0.02): # setup marker generator and color map markers = ('s', 'x', 'o', '^', 'v') colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan') cmap = ListedColormap(colors[:len(np.unique(y))]) # plot the decision surface x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) Z = Z.reshape(xx1.shape) plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) plt.xlim(xx1.min(), xx1.max()) plt.ylim(xx2.min(), xx2.max()) # plot class samples for idx, cl in enumerate(np.unique(y)): plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), edgecolor='black', marker=markers[idx], label=cl)
Описание работы функции plot_decision_regions
Сначала мы определяем цвета и маркеры и затем при помощи ListedColormap создаем из списка цветов палитру (карту цветов). Затем мы определяем минимальные и максимальные значения для двух признаков и на основе векторов этих признаков создаем пару матричных массивов xxl и хх2, используя для этого функцию meshgrid библиотеки NumPy. Учитывая, что мы натренировали наш персептронный классификатор на двупризнаковых размерностях, мы должны сгладить матричные массивы и создать матрицу с тем же самым числом столбцов, что и у тренировочного подмножества цветков ириса, в результате чего можно применить метод predict и идентифицировать метки классов Z для соответствующих точек матрицы. После преобразования формы идентифицированных меток классов Z в матрицу с такими же размерностями, что и у xxl и хх2, можно начертить контурный график, используя для этого функцию contourf библиотеки matplotlib, которая ставит в соответствие разным областям решения разный цвет по каждому идентифицированному классу в матричном массиве.
plot_decision_regions(X, y, classifier=ppn) plt.xlabel('sepal length [cm]') plt.ylabel('petal length [cm]') plt.legend(loc='upper left') plt.tight_layout() plt.show()
'c' argument looks like a single numeric RGB or RGBA sequence, which should be avoided as value-mapping will have precedence in case its length matches with 'x' & 'y'. Please use a 2-D array with a single row if you really want to specify the same RGB or RGBA value for all points.
'c' argument looks like a single numeric RGB or RGBA sequence, which should be avoided as value-mapping will have precedence in case its length matches with 'x' & 'y'. Please use a 2-D array with a single row if you really want to specify the same RGB or RGBA value for all points.
'c' argument looks like a single numeric RGB or RGBA sequence, which should be avoided as value-mapping will have precedence in case its length matches with 'x' & 'y'. Please use a 2-D array with a single row if you really want to specify the same RGB or RGBA value for all points.
В нашем случае удалось найти линию, идеально разделяющую объекты на два класса, однако, чаще всего это невозможно. Фрэнк Розенблатт математически доказал, что в таком случае без установления максимального числа эпох веса никогда не прекратят обновляться, т.е. модель "не сойдётся".
ADALINE
Узнав устройство перцептрона Розанблатта, мы могли заметить несколько проблем этой модели. Основной недостаток — использование ступенчатой функции активации, минимум которой нельзя вычисить аналитически при помощи дифференцирования, т.е. взятия производной. Из-за этого возникает описанная выше проблема — модель принципиально не способная сойтись, если классе неразделимы линейно. Если бы мы могли дифференцировать функцию потерь, как, наприме, OLS-регрессии, то достаточно было бы просто приравнять её дифференциал к нулю, чтобы найти локальный минимум. Так же, видимо, думали Берндард Видроу и его докторант Тэд Хофф, когда через несколько лет, после выхода работ Розенблатта, опубликовали свою статью.
Основное отличие правила обучения ADALINE (также известного как правило Уидроу-Хопфа, или дельта-правило) от правила обучения персептрона Розенблатта в том, что в нем для обновления весов используется линейная функция активации, а не единичная ступенчатая, как в персептроне. В ADALINE эта функция активации представляет собой просто тождественное отображение чистого входа, в результате чего .
Помимо линейной функции активации, которая используется для извлечения весов, далее с целью распознавания меток классов используется квантизатор, аналогичный встречавшейся ранее единичной ступенчатой функции, как проиллюстрировано на нижеследующем рисунке:
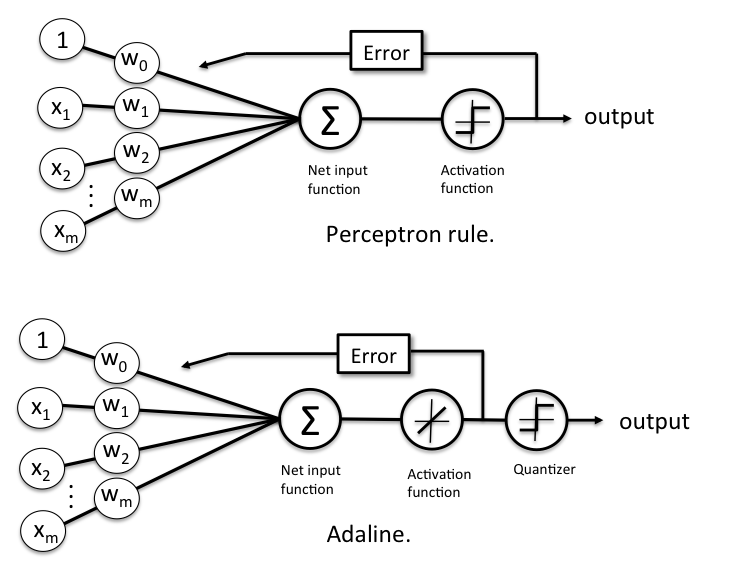
Если сравнить приведенный выше рисунок с иллюстрацией алгоритма обучения персептрона, который мы видели ранее, то ADALINE отличается тем, что вместо бинарных меток классов теперь для вычисления ошибки модели и для обновления весов используется непрерывнозначный выход из линейной функции активации.
Функцией стоимости в случае с ADALINE является сумма квадратичных ошибок (sum of squaгed erroгs, SSE):
Член полусуммы добавлен просто для удобства. Он сократится при взятии производной.
В отличие от единичной ступенчатой функции, основное преимущество этой непрерывной линейной функции активации состоит в том, что функция стоимости становится дифференцируемой и выпуклой, а значит, мы можем легко найти её минимум.
Литература
- V, A. S. (2017, March 30). Understanding Activation Functions in Neural Networks. Medium. https://medium.com/the-theory-of-everything/understanding-activation-functions-in-neural-networks-9491262884e0
Комментарии